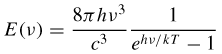Chiunque non rimanga sconvolto dalla meccanica quantiswtica non l'ha pienamente compresa
Niels Bohr
Lord Kelvin nel 1900 annunciò "In questo periodo non esiste niente di nuovo da scoprire in fisica. L'unica cosa che possiamo fare è realizzare esperimenti sempre più precisi". Nessuna previsione penso sia stata tanto smentita dai fatti. Nel 1985 Wilhelm Rontgen iniziò gli studi sui raggi X e nel 1901 fu insignito del premio nobel per la sua scoperta. Agli inizi del '900 Becquerel e i coniugi Curie scoprivano la radioattività, mentre Joseph Thomson scopriva l'esistenza dell'elettrone (preconizzato da George Stoney nel 1891). Nel 1908 Ernest Rutherford ebbe il premio nobel avendo accertato che la radioattività era una spontanea disintegrazione degli atomi che emettevano raggi alfa e beta (in seguito furono individuati i raggi gamma); nel 1907 scoprì l'esistenza del nucleo atomico degli atomi e fu il primo fisico che trasmutò un elemento chimico in un altro, cioè l'azoto in un isotopo di ossigeno mediante la reazione nucleare:
N(14) + a = O(17) + p.
dove per a s'intende la particella alfa, nucleo dell'He(4), e per p s'intende il protone. Mentre lavorava con Niels Bohr, che aveva sviluppato un modello dell'atomo in cui gli elettroni si muovevano in orbite circolari o ellittiche attorno a un nucleo, come in un sistema planetario, Rutherford avanzò una proposta sull'esistenza di particelle neutre, (i neutroni), che potevano compensare l'effetto repulsivo delle cariche positive dei protoni nel nucleo, aumentando le forze nucleari attrattive e impedendo così ai nuclei degli atomi pesanti di disintegrarsi. Nel 1905, con l'avvento delle equazioni di Maxwell, delle trasformazioni di Lorentz e infine della teoria della relatività speciale di Einstein viene meno il concetto, fino ad allora dato per scontato, di tempo assoluto. Il tempo e lo spazio sono legati insieme a formare quello che viene chiamato spaziotempo. Sempre nel 1905 Einstein ontroduce la famosissima formula E = mc^2, l'equazione che stabilisce l'equivalenza e il fattore di conversione tra l'energia e la massa di un sistema fisico. La relatività generale del 1915 postula invece l'uguaglianza della massa gravitazionale e della massa inerziale (quella indotta dall'accelerazione). Nel 1924 nella fisica quantistica viene introdotto lo spin (letteralmente "giro vorticoso" in inglese) e cioè una grandezza, o numero quantico, associata alle particelle, che concorre a definirne lo stato quantico. Lo spin è una forma di momento angolare, avendo di tale entità fisica le dimensioni e, pur non esistendo una grandezza corrispondente in meccanica classica, per analogia richiama la rotazione della particella intorno al proprio asse (viene anche definito come momento angolare intrinseco). A differenza degli oggetti macroscopici però, per i quali il momento angolare è associato alla massa, per lo spin questa non è richiesta: ad esempio i fotoni, che hanno massa a riposo zero, o particelle elementari come gli elettroni, che sono considerate puntiformi, possiedono uno spin. Nel 1932, annus mirabilis per la fisica, Chadwick scopre il neutrone, Anderson il positrone, prima particela di antimateria e Fermi ipotizza l'esistenza dei neutrini.
Non possiamo dimenticare che la fama di Democrito è dovuta alla sua celebre teoria atomista considerata, anche a distanza di secoli, una delle visioni più “scientifiche” dell'antichità: l'atomismo democriteo infatti fu ripreso non solo da altri pensatori greci, come Epicuro, ma anche da filosofi e poeti romani (Lucrezio), nonché da filosofi del tardo medioevo e dell'età rinascimentale. Come è stato rilevato da Theodor Gomperz e da altri studiosi, Democrito può essere considerato il “padre della fisica”, così come Empedocle lo è stato per la chimica. Geymonat afferma che “l’atomismo di Democrito ebbe una funzione determinante, nel XVI e XVII secolo, per la formazione della scienza moderna”.
Al termine di questo breve excursus sulla fisica di inizio XX secolo passo ora a parlare di Meccanica quantistica.
La meccanica quantistica è una teoria fisica relativamente complessa tanto da capire quanto da spiegare. Si afferma, infatti, che non vi sia nessuno capace di comprenderla e che essa determini l'accadere dei fenomeni al di là dell'esperienza umana. Esiste, infatti, una differenza talmente grande tra i nostri comportamenti quotidiani e quelli quantistici che ci risulta impossibile tradurli in immagini ed eventi.
La meccanica quantistica è la teoria fisica che descrive il comportamento della materia, della radiazione e le reciproche interazioni, con particolare riguardo ai fenomeni caratteristici della scala di lunghezza o di energia atomica e subatomica.
Come caratteristica fondamentale, la meccanica quantistica descrive la radiazione e la materia sia come fenomeno ondulatorio che come entità corpuscolare, al contrario della meccanica classica, dove, per esempio, la luce è descritta solo come un'onda e l'elettrone solo come una particella. Questa proprietà, chiamata dualismo onda-particella, è la principale ragione del fallimento di tutte le teorie classiche sviluppate fino al XIX secolo. La relazione fra la natura ondulatoria e quella corpuscolare delle particelle è definita nel principio di complementarità e formalizzata nel principio di indeterminazione di Heisenberg.
La meccanica classica si dimostrò incapace di descrivere il comportamento della materia e della radiazione elettromagnetica a livello microscopico, a scale di lunghezza inferiori o dell'ordine di quelle dell'atomo o a energie nella scala delle interazioni interatomiche. L'incoerenza e l'impossibilità delle leggi classiche di rappresentare la realtà sperimentale, in particolare della luce e dell'elettrone, furono dunque le motivazioni principali che portarono allo sviluppo della meccanica quantistica nella prima metà del XX secolo. Essa nacque unendo ed elaborando un insieme di teorie fisiche formulate a cavallo del XIX e del XX secolo, di carattere spesso empirico. Il nome "teoria dei quanti", introdotto da Max Planck agli inizi del novecento, si basa sul fatto che alcune quantità o grandezze di certi sistemi fisici a livello microscopico, come l'energia o il momento angolare, possono variare soltanto di valori discreti, detti "quanti", e non in modo continuo. (Planck fu il primo a introdurre in fisica la parola quanto).
Gli atomi furono riconosciuti, da John Dalton nel 1803, come i costituenti fondamentali delle molecole e di tutta la materia. Nel 1869 la tavola periodica degli elementi consentì di raggruppare gli atomi secondo le loro proprietà chimiche e questo permise di scoprire leggi di carattere periodico, come la regola dell'ottetto, la cui origine era ignota. La regola enuncia che quando un atomo possiede il livello elettronico esterno completo (detto "guscio di valenza"), costituito da otto elettroni, esso è in una condizione di particolare stabilità energetica, e tende a non formare ulteriori legami. Considerato il fatto che tuttavia il primo livello può contenere al massimo due elettroni, sarebbe meglio parlare di "regola dell'ottetto-duetto".
Gli studi di Avogadro, Dumas e Gauden dimostrarono che gli atomi si compongono fra loro a formare le molecole, strutturandosi e combinandosi secondo leggi di carattere geometrico. Tutte queste nuove scoperte lasciavano non chiariti i motivi per cui gli elementi e le molecole si formassero secondo queste leggi regolari e periodiche. La base della struttura interna dell'atomo venne posta con le scoperte dell'elettrone, da parte di Joseph Thompson, e del nucleo da parte di Rutherford. In base al modello di Rutherford in un atomo un nucleo centrale di carica positiva agisce sugli elettroni negativi in modo analogo a quello con cui il Sole agisce sui pianeti del sistema solare. Tuttavia, le emissioni di energia previste dalla teoria elettromagnetica di Maxwell per cariche in moto accelerato, avrebbero avuto una grande intensità e avrebbero dovuto portare l'atomo a collassare in pochi istanti, in opposizione alla stabilità di tutta la materia osservata. Questa contraddizione, come l'emissione di corpo nero e l'effetto fotoelettrico portarono a dover introdurre il principio dei quanti e della quantizzazione.
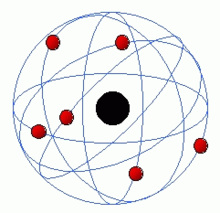
L'atomo di Rutherford, con gli elettroni in rosso e il nucleo in nero
La radiazione elettromagnetica era stata prevista teoricamente da James Clerk Maxwell nel 1850 e rilevata sperimentalmente da Heinrich Hertz nel 1886. Tuttavia, Wien scoprì che, secondo la teoria classica disponibile all'epoca, un corpo nero, in grado di assorbire tutta la radiazione incidente, dovrebbe emettere onde elettromagnetiche con intensità infinita alle corte lunghezze d'onda. Questo devastante paradosso fu ritenuto di grande importanza e fu chiamato nel 1911 "catastrofe ultravioletta".
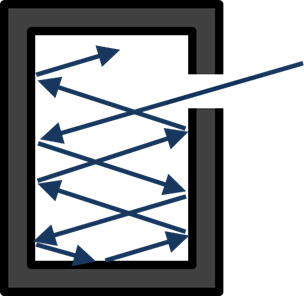
Un corpo nero, oggetto in grado di assorbire tutta la radiazione incidente, può essere realizzato mediante una cavità nera con un piccolo foro. Secondo la previsione classica, questo corpo avrebbe dovuto emettere una intensità infinita di radiazione elettromagnetica ad alta frequenza.
Nel 1887 Heinrich Hertz scoprì che le scariche elettriche fra due corpi conduttori carichi sono molto più intense se questi sono esposti a radiazione ultravioletta. Questo fenomeno, dovuto all'interazione fra la radiazione elettromagnetica e la materia, fu chiamato effetto fotoelettrico. Si scoprì che questo fenomeno inspiegabilmente scompariva del tutto per frequenze della radiazione incidente più basse di un valore di soglia, indipendentemente dall'intensità totale di questa. Inoltre, se si verificava l'effetto fotoelettrico, l'energia degli elettroni emessi dalle piastre conduttrici risultava direttamente proporzionale alla frequenza della radiazione elettromagnetica. Tali evidenze sperimentali non si potevano spiegare con la classica teoria ondulatoria di Maxwell. Per la spiegazione teorica di queste proprietà era necessario introdurre un modello corpuscolare della luce e a Einstein fu assegnato il premio Nobel per la fisica nel 1921, proprio per aver spiegato l'effeto fotoelettrico introducendo un modelo corpuscolare per la radiazione elettromagnetica.
La meccanica quantistica, sviluppandosi con i contributi di numerosi fisici nell'arco di oltre mezzo secolo fu in grado di fornire una spiegazione soddisfacente a molte "contraddizioni!.
Max Planck comprese nel 1900 che se i possibili valori dell'energia delle onde elettromagnetiche fossero discreti, allora il problema del corpo nero potrebbe essere risolto in accordo con i risultati degli esperimenti. Il fisico tedesco introdusse una costante h, chiamata poi in suo onore costante di Planck e con le dimensioni fisiche di energia per tempo [h] = [E][t]. L'introduzione della costante di Planck ha consentito di valutare l'intensità della radiazione elettromagnetica in funzione della sua lunghezza d'onda:
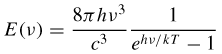
Esssa ha un andamento a campana come quello mostrato nella figura.
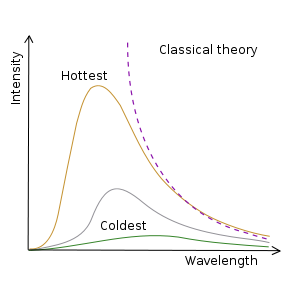
Andamento dell'emissione da un corpo nero, in funzione della lunghezza d'onda, nel caso della fisica classica e di quella quantistica.
La formila di Planck fu utilizzata per spiegare l'effetto fotoelettrico da Einstein, che mostrò come i campi elettromagnetici siano costituiti da particelle o quanti elementari, chiamati, nel 1926, fotoni. La dimensione E di un quanto di energia dipende dalla frequenza f della radiazione secondo la formula E=hf dove h è la costante di Planck. Questa equazione viene per esempio comunemente utilizzata per ricavare l'energia di un fotone. Quando un fotone viene assorbito da un elettrone, questo acquista tutta la sua energia e se questa è abbastanza grande può anche sfuggire all'attrazione dell'atomo a cui è legato. Se l'energia del fotone dipende dalla sua lunghezza d'onda, a frequenze troppo basse l'energia è insufficiente affinché questo processo sia possibile. L'effetto fotoelettrico quindi sparisce del tutto, indipendentemente dal numero di fotoni incidenti (che determinano solo l'ampiezza dell'onda classica). L'interazione fra radiazione e materia viene quindi spiegata in termini di processi puntuali che coinvolgono particelle elementari, concetto fondamentale delle moderne teorie di campo.
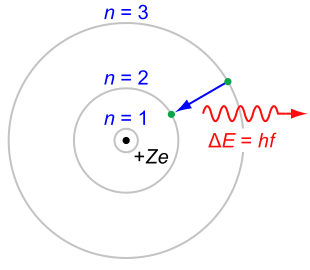
Nel modello di Bohr dell'atomo di idrogeno, un elettrone può percorrere solamente alcune determinate traiettorie classiche. Queste traiettorie sono stabili e discrete, indicate con un numero intero progressivo n = 1, 2, 3. Ogni qual volta l'elettrone scende a una orbita inferiore emette radiazione elettromagnetica, sotto forma di un fotone, di energia corrispondente all'energia persa nel salto da un'orbita all'altra.
Nel 1913 il fisico danese Niels Bohr propose un modello empirico per tentare di riunire le evidenze attorno alla stabilità dell'atomo di idrogeno e al suo spettro di emissione, come l'equazione di Rydberg. Max Planck, Albert Einstein, Peter Debye e Arnold Sommerfeld contribuirono allo sviluppo e alla generalizzazione dell'insieme delle regole formali proposte da Bohr, indicato con l'espressione vecchia teoria dei quanti. In questo modello il moto dell'elettrone nell'atomo di idrogeno è consentito solo su un insieme discreto di orbite chiuse stazionarie stabili di tipo circolare o ellittico. La radiazione elettromagnetica viene emessa o assorbita solo quando un elettrone passa da un'orbita più piccola a una più grande. In questo modo Bohr fu in grado di calcolare i livelli energetici dell'atomo di idrogeno, dimostrando che in questo sistema un elettrone non può assumere qualsiasi valore di energia. L'elettrone al contrario può avere solo alcuni precisi e discreti valori di energia En determinati solo dal numero intero n:
En = -13,36 eV/n^2 (sono valori discreti negativi perché gli elettroni sono legati)
in buono accordo con gli esperimenti e con una energia minima diversa da zero En{min} = - 13,36 eV raggiunta quando n=1. Restava tuttavia da chiarire come mai l'elettrone potesse percorrere solo alcune specifiche traiettorie chiuse.
Nel 1924 il fisico francese Louis de Broglie scoprì che l'elettrone, oltre a essere un corpuscolo, ha anche un comportamento ondulatorio che si può manifestare ad esempio in fenomeni di interferenza. La lunghezza d'onda lambda dell'elettrone vale:
lamda = h/p
dove h è la costante di Planck e p la quantità di moto. In questo modo la legge di quantizzazione imposta da Bohr poteva essere interpretata semplicemente come la condizione di onde stazionarie, equivalenti alle onde che si sviluppano su una corda vibrante di un violino. Sulla base di questi risultati, nel 1925-1926, Werner Heisenberg e Erwin Schrödinger svilupparono rispettivamente la meccanica delle matrici e la meccanica ondulatoria, due formulazioni differenti della meccanica quantistica. L'equazione di Schrödinger in particolare è simile a quella delle onde e le sue soluzioni stazionarie rappresentano i possibili stati delle particelle e quindi anche degli elettroni nell'atomo di idrogeno. La natura di queste onde fu immediato oggetto di grande dibattito, un dibattito che si protrae in una certa misura fino ai giorni nostri. Nella seconda metà degli anni venti, la teoria fu formalizzata, con l'adozione di postulati fondamentali, da Paul Adrien Maurice Dirac, John Von Neumann e Hermann Weyl.
Agli inizi del Novecento si comprese che i nuovi fenomeni scoperti a scale atomiche rendevano necessaria la nascita di una nuova fisica del tutto differente rispetto a quella classica sviluppata fino ad allora.
La meccanica quantistica si è differenziata dalla fisica classica, sviluppata fin dai primi lavori di Galileo e di Isaac Newton, in primo luogo ridefinendo il concetto di misura. La novità rispetto alle precedenti teorie riguarda l'impossibilità di conoscere lo stato di una particella senza perturbarlo in maniera irreparabile (l'osservazione modifica lo stato dell'oggetto osservato). Al contrario della meccanica classica dove è sempre possibile concepire uno spettatore passivo in grado di conoscere ogni dettaglio di un dato sistema, secondo la meccanica quantistica è perfino privo di senso assegnare un valore a una qualsiasi proprietà di un dato sistema senza che questa sia stata attivamente misurata da un osservatore. Le leggi quantistiche stabiliscono che il processo di misura non è descrivibile come la semplice evoluzione temporale del sistema, dell'osservatore e degli apparati sperimentali considerati assieme.
Questo ha come conseguenza il fatto che una volta misurata e determinata con precisione una quantità di un sistema non si può in alcun modo determinare quale fosse il suo valore prima della misurazione. Per esempio secondo la meccanica classica la conoscenza della posizione e della velocità di una particella in un dato istante permette di determinarne automaticamente la sua traiettoria passata e futura con certezza. In meccanica quantistica, viceversa, la conoscenza della velocità di una particella a un dato istante non è sufficiente a stabilire quale fosse il suo valore nel passato. Inoltre acquisire la stessa conoscenza della velocità della particella distrugge ogni altra informazione sulla posizione rendendo anche impossibile il calcolo della traiettoria futura.
La fisica classica fino al XIX secolo era divisa in due corpi di leggi, quelle di Newton, che descrivono i moti e la dinamica dei corpi meccanici, e quelle di Maxwell che descrivono l'andamento e i vincoli a cui sono soggetti i campi elettromagnetici come la luce e le onde radio. A lungo si era dibattuto sulla natura della luce e alcune evidenze sperimentali, come l'esperimento di Young, portavano a pensare che la luce dovesse essere considerata come un'onda.
Alcuni tentativi furono fatti per cercare di riunire tutte le leggi della fisica in una forma unitaria e per risolvere alcune incoerenze presenti nelle due formulazioni. In questo modo nacque la teoria della relatività e la scoperta anche di una natura corpuscolare della luce. Nella natura corpuscolare, avanzata da Einstein e Max Planck, la luce era considerata come composta da fotoni che trasportano quantità discrete dell'energia totale dell'onda elettromagnetica. In modo analogo de Broglie scoprì che anche l'elettrone ha comportamenti ondulatori, come la diffrazione osservata nell'esperimento di Clinton Joseph Davisson e Laster Germer nei cristalli di nichel nel 1926.
Sulla base di questi risultati, Bohr comprese che la natura della materia e della radiazione non doveva essere ricondotta solo in termini esclusivi o di un'onda o di una particella, ma sia l'elettrone che il fotone sono al tempo stesso sia un corpuscolo sia un'onda. Questo concetto, formulato dal fisico danese nel 1928 e noto come principio di complementarità, si basa sul fatto che la descrizione completa dei fenomeni che avvengono alle scale atomiche richiede proprietà che appartengono sia alle onde che alle particelle.
Nella meccanica classica è possibile conoscere con precisione arbitraria e limitata solo dagli apparati sperimentali la posizione e la velocità di una particella, che ad ogni istante determinano un punto nella traiettoria percorsa. Inoltre, quando si misura la posizione della particella, non si modifica in alcun modo la sua velocità. Inoltre due misure immediatamente successive della posizione permettono di determinare approssimativamente la velocità della particella.
Heisenberg nel 1927 mostrò che questa misura classica non è possibile. Nella meccanica quantistica, alcune coppie di quantità fisiche, come velocità e posizione, non possono essere misurate nello stesso momento entrambe con precisione arbitraria. Tanto migliore è la precisione della misura di una delle due grandezze, tanto peggiora la precisione ottenibile nella misura dell'altra. In altri termini, misurare la posizione di una particella provoca una perturbazione impossibile da prevedere della sua velocità e viceversa. In formule:
Delta p . Delta x maggiore o uguale a h/4pi greco
dove Delta x è l'incertezza sulla misura della posizione e Delta p è quella sulla quantità di moto p = m v. Il limite inferiore del prodotto delle incertezze è quindi proporzionale alla costante di Planck h su 4 pi greco.
Heisenberg osservò che per conoscere la posizione di un elettrone, questo dovrà essere illuminato da un fotone. Più bassa sarà la lunghezza d'onda del fotone, maggiore sarà la precisione con cui la posizione dell'elettrone viene misurata. Infatti, anche le comuni onde marine non sono influenzate nella propagazione dalla presenza di piccoli oggetti. Al contrario, oggetti grandi almeno quanto la lunghezza d'onda disturbano e spezzano i fronti dell'onda, disturbi che permettono da soli di individuare la presenza dell'ostacolo che le ha generate. In ambito quantistico tuttavia, a basse lunghezze d'onda il fotone trasporterà un'energia sempre maggiore, che assorbita dall'elettrone ne perturba sempre di più la sua velocità rendendo impossibile stabilire in contemporanea quale sia il suo valore. Al contrario, un fotone ad alta lunghezza d'onda perturberà poco la velocità dell'elettrone ma sarà in grado di determinare con poca precisione la sua posizione.
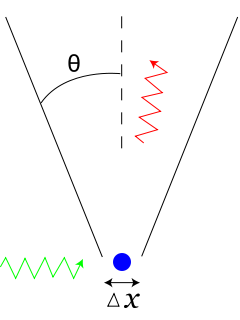
L'esperimento mentale di Heisenberg per la localizzazione di un elettrone. Per conoscere la posizione dell'elettrone questo deve essere illuminato da un fotone, che tuttavia tanto meglio risolve la posizione tanto più perturba la velocità. Il fascio incidente è indicato in verde, quello deviato in rosso, mentre in blu è rappresentato l'elettrone.
L'esperimento delle due fenditure fu ideato originariamente da Thomas Young nel 1803 e Augustin Fresnel agli inizi del XIX secolo per mostrare la natura ondulatoria della luce. Una sorgente di luce viene indirizzata verso due sottili fenditure e produce su di uno schermo una figura di interferenza, già osservata nel medesimo esperimento condotto con onde sulla superficie dell'acqua. Questa figura consiste in una sequenza di bande più luminose intervallate da regioni più scure prive di luce. Questo permise di concludere che la luce ha sicuramente una natura ondulatoria; con particelle classiche infatti si formerebbero solamente due bande in corrispondenza dei due fori delle fenditure.
Per dimostrare la natura ondulatoria delle particelle, lo stesso esperimento è stato condotto nel XX secolo con gli elettroni. In questo caso una sorgente emette un singolo elettrone per volta di fronte a due fenditure e uno schermo dietro di queste segnala con un punto la posizione finale raggiunta. Dopo molti elettroni emessi è possibile osservare la distribuzione dei punti sullo schermo, distribuzione che si presenta analoga a quella di interferenza, con sequenze di bande ricche di punti intervallate da regioni in cui questi sono assenti. In questo caso tuttavia, trattandosi del passaggio di singoli elettroni, si deve concludere che in qualche modo l'elettrone stesso auto-interferisce, come se passasse allo stesso tempo per le due fenditure come un'onda. L'onda in questo caso ha natura probabilistica, in quanto, per poter essere messa in evidenza, richiede la ripetizione dello stesso processo fisico, il passaggio di un singolo elettrone attraverso le due fenditure, un numero N di volte grande, riproducendo esattamente la natura ondulatoria nel limite in cui N è infinito.
Questo risultato lascia tuttavia aperta la questione di come sia possibile che un singolo elettrone si propaghi nello stesso momento attraverso due distinte fenditure. Si può quindi tentare di osservare l'elettrone fisicamente attraversare le due fenditure illuminando queste ultime con la luce. I fotoni che costituiscono la luce colpiranno l'elettrone e permetteranno di capire se un elettrone è passato attraverso una fenditura. In questo esperimento tuttavia si trova che l'elettrone viene rilevato passare solo attraverso una singola fenditura alla volta, ma nello stesso momento non si osserva più la figura di interferenza sullo schermo, ma solo le due bande previste dalla meccanica classica. La misura stessa della posizione e del passaggio dell'elettrone disturba quindi drasticamente il suo stato originario, sulla base del principio di indeterminazione. Non vi è alcun modo di stabilire come si comporti l'elettrone nei pressi delle fenditure che non distrugga al tempo stesso l'interferenza ondulatoria. Come scrisse Feynman illustrando questo esperimento, in qualche modo è come se il principio di indeterminazione protegga la meccanica quantistica e la natura dal mostrare nello stesso momento l'elettrone in un comportamento ondulatorio e in uno corpuscolare:
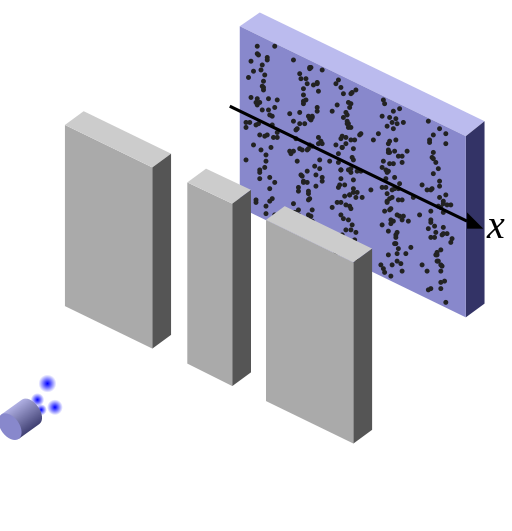
Nell'esperimento, gli elettroni che sono inviati da una sorgente attraverso due fenditure creano sullo schermo figure di interferenza, dimostrando la natura ondulatoria degli elettroni. Secondo la meccanica classica, le particelle dovrebbero invece creare due sole bande in corrispondenza delle due fenditure, non una sequenza alterna di varia intensità. La figura di interferenza è tuttavia distrutta quando un rivelatore del passaggio dell'elettrone viene posto nelle fenditure.
Richard Feynman osservò: «Heisenberg propose, come principio generale, il suo principio di indeterminazione, che noi possiamo formulare in termini del nostro esperimento come segue: "È impossibile progettare un apparato per determinare attraverso quale fenditura l'elettrone passa, che non disturberà allo stesso tempo l'elettrone abbastanza da distruggere la figura di interferenza." »
In questo modo deve essere interpretato il principio di complementarità: entrambe le descrizioni sono necessarie in una descrizione del mondo quantistico, ma nessuna delle due può essere evidenziata nello stesso momento. Non vi è quindi modo di osservare allo stesso tempo l'elettrone come corpuscolo e come onda. Inoltre, fatto essenziale, evidenziato da Bohr, la natura corpuscolare o ondulatoria mostrata di volta in volta è determinata strettamente dall'apparato sperimentale e non direttamente dal sistema fisico oggetto di sperimentazione.
Schrödinger scrisse nel 1926 una serie di articoli in cui mostrò che una meccanica ondulatoria possa spiegare l'emergere di numeri interi e dei quanti, gli insiemi di valori discreti anziché continui permessi per alcune quantità fisiche di certi sistemi (come l'energia degli elettroni nell'atomo di idrogeno). In particolare, basandosi sui lavori di De Broglie, osservò che le onde stazionarie soddisfano vincoli simili a quelli imposti dalle condizioni di quantizzazione di Bohr:
« [...] si può sostituire la regola di quantizzazione usuale con un altro requisito dove non appare più la parola "numeri interi". Piuttosto, gli stessi numeri interi si rivelano naturalmente dello stesso tipo dei numeri interi associati al numero di nodi di una stringa vibrante. Il nuovo punto di vista è generalizzabile e tocca, come credo, molto profondamente la vera natura delle regole quantistiche.»
In un'onda stazionaria, i nodi sono punti che non sono coinvolti dall'oscillazione, in rosso nella figura. Il numero di nodi è quindi sempre intero.
Il numero di nodi in una normale stringa vibrante stazionaria è intero, se questi sono associati alle quantità fisiche come l'energia e il momento angolare allora ne consegue che anche queste devono essere multipli interi di una grandezza fondamentale. Affinché questa equivalenza sia possibile, lo stato fisico deve essere associato a un'onda che vibra e si evolve secondo le condizioni di stazionarietà.
Come Schrödinger stesso osservò, condizioni di tipo ondulatorio sono presenti ed erano già state scoperte anche per la meccanica classica di tipo newtoniano. Nell'ottica geometrica, il limite delle leggi dell'ottica in cui la lunghezza d'onda della luce tende a zero, i raggi di luce si propagano seguendo percorsi che minimizzano il cammino ottico, come stabilito dal principio di Fermat.
Tuttavia l'ottica geometrica non considera gli effetti che si hanno quando la lunghezza d'onda della luce non è trascurabile, come l'interferenza e la diffrazione. Guidato da questa analogia ottico-meccanica, Schrödinger suppose che le leggi della meccanica classica di Newton siano solamente una approssimazione delle leggi seguite dalle particelle, una approssimazione valida per grandi energie e grandi scale come per le leggi dell'ottica geometrica, ma non in grado di catturare tutta la realtà fisica, in particolare a piccole lunghezze, dove come per la luce, fenomeni come l'interferenza e la diffrazione diventano dominanti. Schrödinger postulò quindi una equazione di stazionarietà per un'onda la cui esplicitazione è abbastanza complessa e che, pertanto, trascuro.
In meccanica classica, lo stato di una particella viene definito attraverso il valore esatto delle due quantità osservabili posizione e impulso (dette variabili canoniche); in meccanica quantistica, invece, lo stato di una particella è descritto (nella rappresentazione di Schroedinger) da una funzione d'onda. Essa non ha un proprio significato fisico, mentre lo ha il suo modulo al quadrato, che fornisce la distribuzione di probabilità della posizione: per ogni punto dello spazio, assegna la probabilità di trovare la particella in quel punto, quando si misura la sua posizione. Il significato di questa probabilità può essere interpretato come segue: avendo a disposizione infiniti sistemi identici, effettuando la stessa misura su tutti i sistemi contemporaneamente, la distribuzione dei valori ottenuti è proprio il modulo al quadrato della funzione d'onda. Similmente, il modulo al quadrato della trasformata di Fourier della funzione d'onda fornisce la distribuzione di probabilità dell'impulso (variazione della quantità di moto mv in un intervallo di tempo) della particella stessa. (La trasformata di Fourier è uno degli strumenti matematici maggiormente utilizzati nell'ambito della fisica. Essa permette di scrivere una funzione dipendente dal tempo nel dominio delle frequenze. Questa rappresentazione viene chiamata spesso spettro della funzione).
In generale, la teoria quantistica dà informazioni sulle probabilità di ottenere un dato valore quando si misura una quantità osservabile (a volte, si può ottenere un preciso valore con la probabilità del 100%). Per le proprietà della trasformata di Fourier, tanto più la distribuzione di probabilità della posizione di una particella è concentrata (la particella quantistica è ben localizzata), tanto più la distribuzione degli impulsi si allarga, e viceversa. Si tratta di una manifestazione del principio di indeterminazione di Heisenberg: è impossibile costruire una funzione d'onda arbitrariamente ben localizzata sia in posizione che in impulso.
Alcune funzioni d'onda descrivono distribuzioni di probabilità che sono costanti nel tempo. Molti sistemi trattati in meccanica classica possono essere descritti da queste onde stazionarie. Ad esempio, un elettrone in un atomo non eccitato è descritto classicamente come una particella che ruota attorno al nucleo dell'atomo, mentre in Meccanica quantistica essa è descritta da un'onda stazionaria che presenta una determinata funzione di distribuzione dotata di simmetria sferica rispetto al nucleo. Questa intuizione è alla base del modello atomico di Bohr.
Benché la presenza di una funzione d'onda non permetta di prevedere a priori il risultato, ogni misura porta comunque a ottenere un valore definito (e non per esempio un valore medio). Questo problema, che viene spesso chiamato problema della misura, ha dato vita ad uno dei più profondi e complessi dibattiti intellettuali della storia della scienza.
Ad esempio consideriamo una particella che si muove liberamente nello spazio, con certe distribuzioni di probabilità per posizione e velocità e supponiamo di misurare la sua posizione, ottenendo un certo valore x. Allora, si può prevedere che una successiva misura di posizione (abbastanza vicina nel tempo) porterà certamente allo stesso risultato appena ottenuto: la funzione d'onda è collassata in un punto, fornendo a quel punto la probabilità certa.
Il collasso della funzione d'onda all'atto della misura non è descritto dall'equazione di Schrödinger, che stabilisce solo l'andamento dell'evoluzione temporale. Questa è, infatti, strettamente deterministica, in quanto è possibile prevedere la forma della funzione d'onda a un qualsiasi istante successivo. La natura probabilistica della meccanica quantistica si manifesta, invece, all'atto della misura.
Il principio di indeterminazione di Heisenberg porta inoltre al concetto di osservabili incompatibili: si tratta di coppie di osservabili in cui la conoscenza completa di una delle due porta alla completa mancanza di conoscenza sull'altra. Nel caso precedente, una misura di posizione porta alla completa ignoranza sulla velocità. Allo stesso modo sono incompatibili l'energia e l'intervallo di tempo nel quale tale energia è scambiata. Detto in altre parole, il collasso della funzione d'onda associata a un'osservabile, porta a una funzione di distribuzione uniforme, su tutto il dominio di definizione, per l'osservabile ad essa coniugata.
Per concludere, la limitazione che ci impone il principio di intedeterminazione ci porta a sostituire la certezza con la probabilità. Non possiamo sapere dove sia una particella ma dove è più probabile che si trovi. Nonostante il successo della meccanica quantistica, nel momento di descrivere e prevedere eventi, gli stessi fondatori si trovavano a disagio per quanto riguardare l'interpretazione di tali risultati. Se l'unica cosa che si può misurare sono le probabilità, se il principio di indeterminazione ci pone limiti su ciò che possiamo misutrare, se la dualità onda-partiicella ci permette di osservare un sistema come onda o come particella, ma non come entrambe nello stesso tempo ... allora dove è finita l'obiettività della fisica? Bohr e Heisenberg affermarono che la funzione d'onda probabilistica rappresenta tutto ciò che possiamo sapere di un sistema e che quello che non possiamo estrarre da essa è come se non esistesse. Non ha senso chiedersi dove sia la particella prima di misurarne la posizione. Il concetto stesso di posizione cessa di avere senso, dal momento che c'è una probabilità reale che la particella si trovi in una qualsiasi posizione. Solo quando la si misura, la funzione d'onda collassa e assume un valore concreto. In un certo senso, la particella sceglie la propria posizione solo quando è osservata e non prima.
BIBLIOGRAFIA
G. Vatinno, Il Nulla e il Tutto. Le meraviglie del possibile, Armando editore, 2012
W. Heisenberg, Fisica e filosofia, il Saggiatore, 1958
Eugenio Caruso - 26-11-2015

IMPRESA OGGI
Dacci una mano!!!!! :)
Un clic sulla striscia pubblicitaria in alto. Grazie!!