Dopo aver analizzato le ricerche e le evidenze della cosmologia moderna è interessante approfondire quali erano le teorie dei cosmologi antichi, anche dell'era pre-socratica; alcune intuizioni di allora ci lasciano stupiti.
Le idee cosmologiche diffuse tra i Greci dell'epoca arcaica sono ricavabili dai poemi omerici. La Terra era concepita come un disco piatto circondato dal fiume Oceano. Al di sopra del disco, in forma di calotta semisferica, era posto il Cielo, mentre al di sotto vi era il Tartaro. Poiché il Tartaro è sempre buio, il Sole e gli altri astri non potevano mai raggiungerlo. (Tartaro, in greco antico Tártaros, indica, nella Teogonia di Esiodo, il luogo inteso come la realtà tenebrosa e sotterranea, e quindi il dio che lo personifica, venuto a essere dopo Caos e Gea. Zeus vi rinchiuse i Titani, stirpe divina e padri degli dei dell'Olimpo, dopo averli sconfitti a seguito della Titanomachia. Lì, inoltre, si trovavano altri mostri come, ad esempio, le Arai, ma anche mortali puniti per i loro gravi misfatti come Tantalo - re della Lidia, punito dagli dei per le sue colpe con una fame e una sete insaziabili: sebbene avesse accanto a sè frutti e acqua, non appena tentava di afferrarli questi si allontanavano da lui. Sempre in Esiodo, Tartaro è considerato il procreatore, insieme con Gaia, di Tifone.).
Secondo una tradizione riferita da Ateneo, e presente già nella mitologia egizia, il Sole durante ogni notte sarebbe stato trasportato da Ovest ad Est lungo l'Oceano, adagiato in un letto o, secondo altri autori, posto in una coppa. Omero conosce e nomina alcune costellazioni e stelle, ma le nozioni astronomiche da lui usate sono estremamente limitate. Esiodo, in relazione alla regolazione dei tempi del lavoro agricolo, ha l'occasione di citare qualche nozione in più. Ad esempio come punti di riferimento temporali usa, sia i solstizi, sia fenomeni stellari. Si tratta però anche in questo caso di conoscenze empiriche, inquadrate nell'ambito della cosmologia tradizionale.
Colui che è tradizionalmente considerato l'iniziatore della filosofia greca, Talete, fondatore della scuola ionica, si occupò anche di astronomia. Gli sono attribuiti una buona stima del diametro apparente del Sole e della Luna (come la 720ª parte del circolo percorso dal Sole), lo studio di solstizi ed equinozi e anche la previsione di un'eclissi solare.
Anassimandro (anche lui vissuto tra il VII ed il VI secolo a.C.), che può forse essere considerato il vero iniziatore dell'astronomia razionale, riteneva il mondo un cilindro posto al centro dell'universo con i corpi celesti che vi ruotano attorno, supponendo l'esistenza di mondi infiniti in tutte le direzioni, e avendo così la prima intuizione del principio cosmologico. Sostenne cioè che il cielo fosse anche sotto i nostri piedi, che gli astri si estendono in tutte le direzioni e che tramontano ad Ovest per risorgere ad Est perché ruotano attorno alla Terra. Ad Anassimandro è stata attribuita anche l'invenzione dello gnomone per rilevare l'altezza del Sole e della Luna e quindi l'inclinazione dell'eclittica.
Iceta di Siracusa fu il primo ad asserire che «la terra si muove secondo un circolo», cui farà eco anche Ecfanto di Siracusa che sosteneva la rotazione della terra sul proprio asse secondo un moto apparente del sole da oriente verso occidente.
Contributi essenziali furono quelli di Parmenide, al quale sono attribuiti sia la scoperta della sfericità della terra che la comprensione della causa delle fasi lunari. Parmenide capì che la Luna è sempre piena e sferica e che l'apparenza del suo crescere e decrescere è dovuta al variare della posizione relativa di Terra, Sole e Luna, che rende variabile la porzione della Luna che è illuminata dal Sole e allo stesso tempo è a noi visibile.
Un contributo interessante allo sviluppo delle idee astronomiche venne da Filolao, della scuola di Pitagora, che sostenne un modello di sistema solare non geocentrico: al centro dell'universo vi sarebbe stato un grande Fuoco primordiale, detto Hestia, intorno al quale ruotavano la Terra, l'Antiterra, la Luna, il Sole, Mercurio, Venere, Marte, Giove e Saturno. L'esistenza dell'antiterra fu introdotta probabilmente per giustificare l'invisibilità del fuoco centrale che veniva occultato da quest'ultima, nonché dalla necessità filosofica di arrivare ad un numero totale di dieci corpi, cifra ritenuta sacra nella tetraktys pitagorica. I pitagorici concepivano infatti l'universo come un cosmo, cioè un insieme razionalmente ordinato che rispondeva ad esigenze esoteriche e religiose, nel quale i pianeti compiono movimenti armonici secondo precisi rapporti matematici, generando un suono sublime e celestiale.

Hestia, Terra e Antiterra nel modello pitagorico dell'universo
Platone ebbe dapprima una visione dell'universo eliocentrica, poi ritrattata in tarda età per il geocentrismo. Intuì tuttavia la sfericità della Terra, sostenendo anche che la Luna ricevesse luce dal Sole, e prefigurando il concetto di «grande anno» che da lui prende il nome, ossia della ciclicità degli eventi cosmici.
Eudosso di Cnido sviluppò il concetto di sfere omocentriche, ossia di un universo diviso in sfere aventi un unico centro di rotazione in cui si trovava la Terra; su ogni sfera vi era poi incastonato un pianeta con un moto circolare ed uniforme differente da quello degli altri. In questo modo diede spiegazione dei movimenti retrogradi e degli stazionamenti periodici dei pianeti: per le stelle fisse fu facile attribuire una sfera mobile attorno alla terra immobile, mentre per i pianeti e per la Luna il moto veniva spiegato con una prima sfera che induceva un moto diurno, un'altra per il moto mensile ed infine una terza ed una quarta con diverso orientamento dell'asse per il moto retrogrado. Tenendo conto che il Sole ne possedeva tre, si giunge ad un sistema di ben 27 sfere. Callippo di Cizico aggiunse altre 7 sfere al sistema di Eudosso, portando il totale a 34 sfere, per spiegare le evidenze osservative, relative in particolare alle variazioni di velocità angolare del Sole e della Luna.
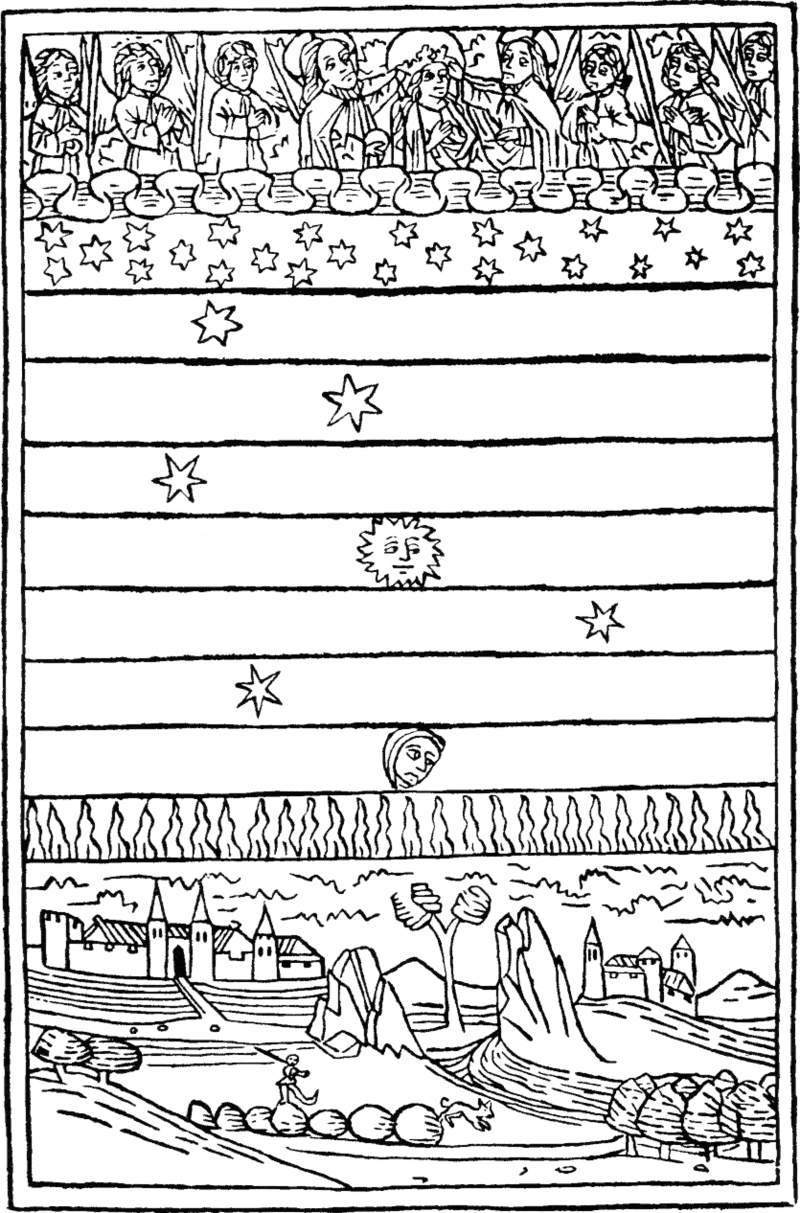
I diversi livelli della cosmologia aristotelica (da un'incisione del 1475): in basso, il mondo sublunare è costituito dai quattro elementi: terra, acqua, aria, più il fuoco, ad uno strato superiore, con lingue fiammeggianti che tendono verso l'alto. Seguono la Luna, i due pianeti interni (Venere e Mercurio), il Sole, i tre pianeti esterni (Marte, Giove e Saturno) e infine le stelle del firmamento, sotto quello che nell'iconografia medioevale sarà il trono di Dio.
Aristotele attribuì realtà fisica alle sfere di Eudosso e Callippo, aggiungendone ancora altre. Egli ipotizzò così un complicato sistema di 55 sfere che rendesse maggiormente ragione delle irregolarità delle traiettorie dei pianeti (in greco plànetes, che significa appunto «errante», per distinguerli dalle altre stelle dette «fisse» perché dotate di moto regolare). Secondo Aristotele, mentre la Terra è formata da quattro elementi (terra, acqua, aria e fuoco), ciò che si trova oltre di essa è composto di un quinto elemento (o essenza): l'etere, privo di massa, invisibile e, soprattutto, eterno e inalterabile. Queste due ultime caratteristiche sanciscono un confine tra i luoghi sub-lunari del mutamento (la Terra), e i luoghi immutabili (il cosmo).
Ogni elemento ha la tendenza a rimanere o a tornare nel proprio luogo naturale, che per la terra e l'acqua è il basso, mentre per l'aria e il fuoco è l'alto. La Terra come pianeta, quindi, non può che stare al centro dell'universo, essendo formata dai due elementi tendenti al basso, ed il "basso assoluto" è proprio il centro dell'universo. Nelle sfere eteree vi erano invece collocate, secondo la concezione astronomica greca fatta propria anche da Platone, in ordine la Luna, Mercurio, Venere, il Sole, Marte, Giove, Saturno, ed infine il cielo delle stelle fisse o Primo mobile, che metteva tutte le altre sfere in movimento. Questo risulta mosso direttamente dalla causa prima o Motore immobile, identificabile con la divinità suprema (mentre le altre divinità risiedevano all'interno del cosmo), in una maniera tuttavia non meccanica o causale, dato che Dio, essendo «atto puro», è assolutamente immobile, oltre ad essere privo di materia e quindi non localizzabile da nessuna parte. Il primo mobile piuttosto si muove per un desiderio di natura intellettiva, cioè tende a Dio come propria causa finale. Cercando di imitare la sua perfetta immobilità, esso è contraddistinto dal moto più regolare e uniforme che ci sia: quello circolare.
Dal Primo mobile partiva poi l'impulso al moto di tutte le altre sfere; a causa tuttavia dell'attrito, che contribuiva a creare un moto differente per ogni sfera, il movimento si corrompeva progressivamente trasformandosi da circolare-uniforme in rettilineo. In tal modo veniva fornita una spiegazione astrologica al divenire terrestre, in un'ottica tipica peraltro di tutta l'astronomia greca, che riconducesse l'origine dei mutamenti a cause non solamente meccaniche, ma soprattutto finalistiche, cioè dotate di senso e destino.
suoi scritti, insieme ai Fenomeni di Euclide, furono tra le prime opere giunte fino a noi nelle quali vi sono applicazioni della matematica all'astronomia. Si tratta però di opere elementari, nelle quali ci si limita ad applicare semplici concetti di geometria sferica ai fenomeni astronomici dovuti alla rotazione diurna. Il “Copernico dell'antichità”: Aristarco di Samo: Aristarco di Samo perfezionò la visione dell'universo di Eraclide Pontico spostando il Sole al centro dell'universo; il moto dei corpi quindi diveniva più semplice da spiegare anche se non ancora perfetto, data la mancata applicazione delle orbite ellittiche. Inoltre, considerò il moto rotatorio della Terra su un asse inclinato, spiegando così le stagioni.
Aristarco fu anche famoso per il metodo di misura della distanza tra la Terra-Sole. Al primo quarto di Luna, quando risulta visibile anche il Sole, i due astri formano un angolo di 90°. Considerando l'ipotetico triangolo tra i tre corpi, Aristarco misurò quello della Terra con la Luna e il Sole, trovando un valore di 87°. In questo modo, con un semplice calcolo trigonometrico ottenne che la distanza Terra-Sole era 19 volte maggiore di quella tra la Terra e la Luna. Il valore in verità è di 400 volte, ma l'importanza di tale misura non consiste nella precisione riscontrata, quanto nel metodo usato e nell'intuizione.
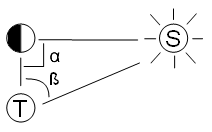
L'unica opera pervenuta di Aristarco è il breve trattato Sulle dimensioni e distanze del Sole e della Luna, nel quale stima la grandezza del Sole e della Luna e calcola le relative distanze dalla Terra.
Terra, Luna e Sole durante una quadratura
Quando la Luna è in quadratura, ossia è illuminata per metà, essa, con la Terra e il Sole, forma il triangolo rettangolo mostrato in figura. Misurando in tale condizione l'angolo ß compreso tra la direzione Terra-Sole e la direzione Terra-Luna è possibile calcolare il rapporto tra le loro distanze mediante ragionamenti di tipo geometrico. Il problema risolto da Aristarco, di calcolare (o meglio, stimare sia per eccesso che per difetto) il rapporto tra i cateti di un triangolo del quale si conoscono gli angoli nel nostro linguaggio è quello di calcolare, o stimare, la tangente trigonometrica di un angolo. L'opera di Aristarco può pertanto essere considerata una delle prime opere di trigonometria.
Aristarco stimò il rapporto tra le distanze del Sole e della Luna come compreso tra 18 e 20, mentre il rapporto tra le distanze medie è in realtà circa 400. Le stime di Aristarco sono correttamente dedotte dal valore da lui assunto per l'angolo Sole-Terra-Luna all'atto della quadratura, ma l'angolo era stato misurato con scarsa precisione. La grandezza abnorme dell'errore è dovuta a due cause principali. In primo luogo Aristarco dovette calcolare la tangente di un angolo molto vicino a un angolo retto, molto vicino cioè al valore nel quale la tangente diverge. In queste condizioni un errore relativamente piccolo sull'angolo si traduce necessariamente in un errore enormemente maggiore sulla tangente. Inoltre per stimare con accuratezza l'angolo che interessava Aristarco occorre riconoscere l'effettiva quadratura con una precisione difficilmente raggiungibile ad occhio nudo. Basta un errore di poche ore sull'istante in cui la quadratura ha luogo perché l'errore sull'angolo si traduca in un errore enorme sulla sua tangente.
Il metodo di Aristarco permette comunque di stimare la tangente di qualsiasi angolo e in questo è probabilmente il maggior valore matematico della sua opera.
L'uso del quadrante per misurare l'altezza degli astri, forse risalente già ai Caldei e ai Babilonesi, è attribuito a diversi astronomi greci come Eratostene ed Ipparco di Nicea
Lo scienziato che per primo misurò la lunghezza del meridiano terrestre fu Eratostene di Cirene, in Egitto. Il metodo che adottò per misurare la lunghezza del meridiano terrestre ebbe come riferimento due città: Alessandria e Siene, l'odierna Assuan. Partendo dall'ipotesi che fossero sullo stesso meridiano (in realtà sono separate da 3° di longitudine), misurò dapprima la distanza tra le due città, ponendo concettualmente i raggi solari paralleli tra loro: questa situazione è possibile in alcuni giorni dell'anno; il giorno del solstizio d'estate, infatti, a Siene il Sole è allo zenit e i raggi risultano verticali, mentre ad Alessandria formano un certo angolo: questo angolo corrisponde all'angolo posto ipoteticamente al centro della Terra tra le rette che congiungono le due città. Il suo valore era di 1/50 di angolo giro (ancora i gradi sessagesimali non erano stati ufficialmente introdotti), che equivaleva a 250.000 stadi, ossia a 39.400 km (contro i 40.000 reali). Un altro importante astronomo greco contemporaneo a Eratostene fu Critodemo, autore dell'???as?? (Visione), opera utilizzata come fonte da Plinio il Giovane e Vettio Valente.
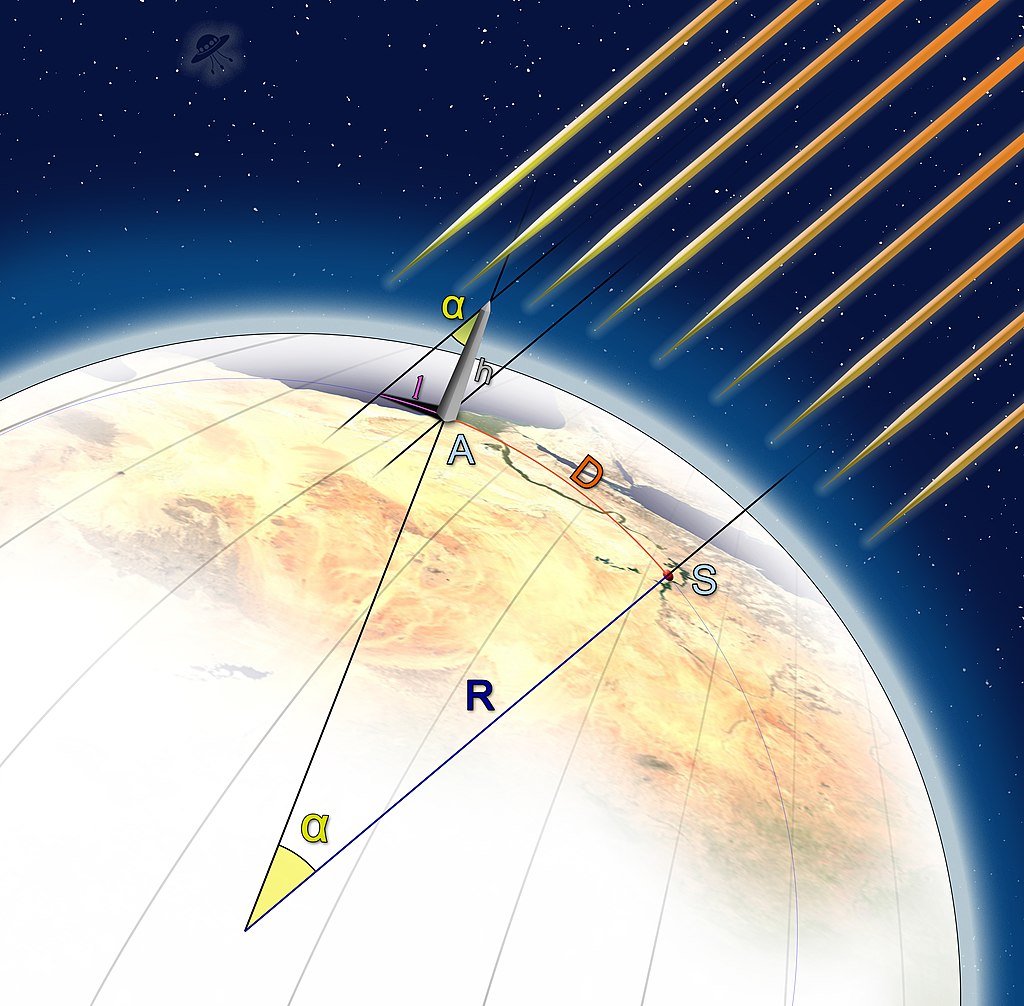
Il metodo utilizzato da Eratostene per misurare il meridiano terrestre è andato perduto; a essere pervenuta è invece una versione divulgativa e semplificata, riportata da Cleomede. Cleomede invita a prendere in considerazione due città, Alessandria d'Egitto e Siene, l'odierna Assuan:
Cleomede assume la distanza delle due città pari a 5.000 stadi egizi;
fa l'ipotesi semplificativa che Siene si trovi esattamente sul Tropico del Cancro;
fa l'ulteriore ipotesi semplificativa, che Siene e Alessandria siano sullo stesso meridiano.
Sotto queste ipotesi, a mezzogiorno del solstizio d'estate a Siene il sole si troverebbe allo zenit, con i raggi del sole perfettamente verticali, in quanto il Tropico del Cancro è proprio il parallelo che unisce i punti con questa caratteristica. In quello stesso giorno, l'angolo di incidenza dei raggi solari misurato ad Alessandria corrisponde all'angolo con il vertice al centro della Terra contenuto tra le semirette che lo congiungono alle due città (ipotesi che le due città siano sullo stesso meridiano). Il suo valore era di 1/50 di angolo giro, di conseguenza la misura dell'intera circonferenza terrestre era di 250.000 (= 50 x 5.000) stadi egizi (1 stadio egizio = 157.5 metri), quindi 39.375 km (contro i 39.941 reali della circonferenza polare) con l'errore dell'1,4% circa.
Apollonio di Perga (città nei pressi della moderna Antalia in Turchia) introdusse il modello eccentrico, secondo cui la Terra non è perfettamente al centro dell'orbita dei corpi celesti. Per spiegare le persistenti differenze osservative, tuttavia, dovette introdurre anche il sistema degli epicicli e dei deferenti (che come caso particolare comprendeva anche il modello eccentrico). I pianeti così avrebbero dovuto ruotare con velocità costante su un'orbita circolare chiamata "epiciclo", mentre il centro della stessa orbita avrebbe ruotato attorno alla Terra percorrendo un cerchio immateriale detto "deferente". Con questi accorgimenti la rotazione dei pianeti poteva essere descritta con modelli matematici molto vicini alla realtà, capaci di riprodurre moti retrogradi e persino variazioni di distanza e luminosità del pianeta.
Ipparco di Nicea utilizzando vecchie osservazioni e cataloghi stellari primordiali, ne creò uno nuovo con 850 stelle, assegnandovi per primo le coordinate ellittiche. Classificò quindi le stelle in una scala di sei grandezze che oggi conosciamo come magnitudini stellari. Tramite questi elementi Ipparco avrebbe notato che tra le sue osservazioni e quelle del passato vi era una certa differenza; questo implicava lo spostamento del centro di rotazione del cielo, e quindi la precessione degli equinozi che compiva un giro completo durante il grande «anno platonico». Il suo studio fu così accurato che poté calcolare i valori di spostamento supposti in 45” d'arco all'anno (oggi il valore stimato è di 50”). Stabilì con buona precisione la differenza tra anno tropico e sidereo calcolandone anche i tempi.
L'universo geocentrico di Tolomeo, che prevede quattro cerchi sublunari (terra, acqua, aria, fuoco) e nove cerchi astrali (Luna, Venere, Mercurio, Sole, Marte, Giove, Saturno, Stelle fisse, Primo mobile) La fama di Claudio Tolomeo, un matematico greco che lavorò ad Alessandria d'Egitto romano nel II secolo, è dovuta a diverse opere sull'astronomia e sull'astrologia, che comprendono l'Almagesto, le Ipotesi planetarie, il Tetrabiblos, nonché le Tavole manuali, l'Iscrizione Canonica e altre minori. I libri dell'Almagesto (Mathematikè Syntaxis) sono un riepilogo di tutto il sapere del passato ed erano talmente completi da divenire in breve tempo un riferimento duraturo per i secoli futuri. In essi Tolomeo riprese e riadattò le vecchie teorie astronomiche alle nuove scoperte: stabilì il sistema geocentrico come punto irremovibile delle sue idee, dal quale giustificò il moto dei pianeti con le teorie di Apollonio ed Ipparco usando epicicli e deferenti; e nel cercare di creare un modello quanto più preciso possibile, ma soprattutto che non differisse dalle osservazioni, introdusse il concetto di equante, perfezionando l'ipotesi dell'eccentrico di Apollonio.
Con questo “stratagemma” Tolomeo riuscì a non discostarsi troppo dai principi aristotelici di circolarità delle orbite e di costanza del moto; difatti, l'eccentricità fa apparire il moto degli astri non costante quando osservato dalla Terra, mentre in realtà risulterebbe continuo. Fu anche con questo sistema che riuscì a giustificare tutti i moti dei pianeti, compresi quelli retrogradi, rispetto alla volta celeste. E per ovviare al fatto che persino le stelle fisse possedevano un lento moto irregolare, dovuto alla precessione degli equinozi scoperta da Ipparco, introdusse un nono cielo al di sopra di esse, identificandolo col primo mobile aristotelico.
«Tolomeo poi, acorgendosi che l'ottava spera si movea per più movimenti, veggendo lo cerchio suo partire dallo diritto cerchio, che volge tutto da oriente in occidente, constretto dalli principii di filosofia, che di necessitade vuole uno primo mobile semplicissimo, puose un altro cielo essere fuori dello Stellato, lo quale facesse questa revoluzione da oriente in occidente: la quale dico che si compie quasi in ventiquattro ore, e quattordici parti delle quindici d'un'altra, grossamente asegnando.»
(Dante Alighieri, Convivio, II, 3, 5)
Tolomeo creò inoltre un catalogo stellare con 1.028 stelle usando le carte di Ipparco con cui divise il cielo in costellazioni, tra le quali le 12 dello zodiaco, usando il metodo delle magnitudini stellari. Il grande lavoro di Tolomeo, la sua fama, le sue conoscenze della matematica e il grande lavoro, posero, per molti secoli, nel cassetto della fantasia qualunque ipotesi geocentrica.
IMPRESA OGGI - Eugenio Caruso - 12- 11- 2020






