Zenone e i suoi paradossi

LA VITA
Zenone di Elea (in greco antico: Zénon; 489 a.C. – 431 a.C.) è stato un filosofo presocratico della Magna Grecia e membro della Scuola eleatica fondata da Parmenide. Aristotele lo definisce inventore della dialettica. È conosciuto soprattutto per i suoi paradossi, che Bertrand Russell definì come «smisuratamente sottili e profondi». Anche per Zenone l'unica immagine che possediamo è quella contenuta nel racconto platonico del Parmenide, nel quale un quarantenne Zenone, «ben fatto e gradevole a vedersi» accompagna Parmenide ad Atene. In base a questo racconto la nascita di Zenone andrebbe collocata nel 490 o subito dopo. Secondo Diogene Laerzio Apollodoro collocava l'acme di Zenone nell'Olimpiade 79 (464-461), facendone risalire la nascita alla fine del secolo precedente.
Non conosciamo nessuna vicenda della sua vita, a meno che si voglia dare valore storico alla narrazione del Parmenide platonico e alla notizia in esso contenuta che Zenone era l'amante di Parmenide. Apollodoro ne faceva invece il figlio adottivo di Parmenide e Ateneo protestava contro quella che considerava un'interpretazione maligna e gratuita di Platone.Una tradizione dice che Zenone non abbandonò mai Elea e in particolare non si recò ad Atene: potrebbe trattarsi di una reazione alla versione platonica. Un altro insieme di notizie concerne le vicende politiche di Zenone, che sarebbe stato fiero oppositore e anche vittima di un tiranno.

IL PENSIERO
A Zenone di Elea, che la tradizione raffigurava come scolaro di Parmenide, sono stati spesso attribuiti gli aspetti più paradossali dell'eleatismo. Isocrate lo collocava vicino a Protagora, Gorgia e Melisso, come rappresentante di una cultura oratoria brillante ma poco utile, e diceva di lui che «tentava di mostrare che le medesime cose sono una volta possibili e poi di nuovo impossibili».
Secondo la testimonianza platonica Zenone dichiarava di esser venuto in aiuto di Parmenide seguendo una via indiretta: contro coloro che mettevano in luce le conseguenze ridicole e contraddittorie delle dottrine parmenidee, mostrava che è invece la molteplicità a produrre risultati contraddittori, facendo apparire «le stesse cose simili e dissimili, una sola e molte, immobili e in movimento». L'interpretazione platonica sembra una correzione dell'immagine paradossale che troviamo in Isocrate. E possibile che l'interpretazione di Platone abbia radici all'interno del gruppo platonico, e all'interpretazione platonica si ricollegava Aristotele quando faceva di Zenone «l'inventore della dialettica». Qui 'dialettica' va intesa probabilmente in senso aristotelico, come un ragionamento che parte da assunzioni altrui e le esamina, per metterne in luce eventuali conseguenze poco credibili.
Già le interpretazioni antiche di Zenone dovevano essere discordanti: l'immagine che ne aveva dato Platone dovette restare canonica, anche se Eudemo, Alessandro e Simplicio la dovevano intendere in modi diversi.Secondo Simplicio, Zenone «nel suo scritto apportava molti argomenti confutatori per mostrare che chi sostiene che esistono molte cose si trova ad asserire cose contrarie, per esempio che le cose sono grandi e piccole, grandi fino ad essere infinite e piccole fino a non avere grandezza». Da una stessa premessa, «i molti sono», Zenone ricavava cioè coppie di conclusioni contraddittorie: i molti sono infinitamente grandi e infinitamente piccoli, hanno molteplicità limitata e molteplicità infinita.
Forse Zenone formulava un primo argomento contro la molteplicità per mostrare che ciascuna delle cose molteplici, se deve essere una e identica a se stessa, non può avere grandezza. Simplicio non ci riferisce questa argomentazione, ma essa doveva introdurre la divisione in parti, che ha tanta importanza nelle argomentazioni zenoniane.
Se ha grandezza, una cosa può esser divisa in parti; ma allora non sarà più unitaria né identica a se stessa, perché sarà costituita da una somma di parti e sarà identica a questa somma. Può darsi che a questo punto Zenone prendesse in considerazione una possibile obiezione alla tesi che per esistere un'unità non deve avere grandezza: se non ha grandezza, una cosa non esiste, perché, per esistere, deve far aumentare la cosa cui è aggiunta o diminuire quella da cui è tolta. Ma Zenone faceva di nuovo intervenire la divisione in parti nel suo secondo argomento contro la molteplicità: se si ammette che ciò che è, per essere, deve avere grandezza, allora si avrà una molteplicità, ma i molti saranno piccoli e grandi. Infatti ogni cosa che è avrà grandezza e spessore, e l'avranno anche ciascuna delle sue parti, ognuna delle quali si distinguerà da un'altra, la quale a sua volta avrà grandezza, spessore e si distinguerà da un'altra; e così via.
Si avranno allora cose tanto piccole da non avere grandezza e tanto grandi da essere infinite. Infatti, via via che si procede nella divisione di una cosa, le sue parti si fanno sempre più piccole, fino quasi ad annullarsi. Ma se ogni cosa è costituita da infinite parti, aventi ciascuna una grandezza, essa sarà infinitamente grande.
Si è osservato che, dal punto di vista matematico, il ragionamento zenoniano non è corretto perché, se le parti alle quali mette capo la divisione all'infinito tendono a 0, allora la loro somma non può essere infinita, in quanto la somma di una serie che converge a 0 (come 1/2, 1/4, 1/8,...) è 1. In questo caso nessuna delle parti è nulla e la loro somma può coincidere con la cosa di cui sono parti. Zenone però riteneva che le parti prodotte dalla divisione fossero non nulle solo se potevano far cambiare la grandezza di una cosa cui fossero aggiunte o tolte, e probabilmente ricavava di qui l'immagine di una somma di infinite parti uguali, una somma appunto infinita.
In questo caso le cose finite diventerebbero somme infinite di parti. Ma è stato anche osservato che nel secondo argomento Zenone poteva formulare non un'antinomia (se si ammette la molteplicità, questa sarà contemporaneamente nulla, perché fatta di parti praticamente uguali a 0, e infinita, perché costituita dalla somma di infinite parti uguali e non nulle), ma un dilemma: o si accetta il primo argomento, e allora le parti alle quali mette capo la divisione, se esistono, non hanno grandezza, sicché la cosa costituita dalla loro somma sarà piccola (dove 'piccolo' è inteso in opposizione a 'grande'); oppure le cose diventano infinitamente grandi, perché sono la somma infinita di infinite parti che hanno grandezza. In questa interpretazione il ragionamento di Zenone sarebbe meno dipendente da una divisione in parti rappresentabile come una serie.
Probabilmente nel formulare i suoi ragionamenti Zenone non dava un'interpretazione geometrica delle cose, ma spingeva oltre ogni limite un processo di divisione che ai suoi primi stadi aveva ovvi riscontri intuitivi. Doveva esser questo il presupposto del terzo argomento contro la molteplicità, che Simplicio dice di riferire alla lettera: «se i molti sono, è necessario che siano tanti quanti sono; e se sono tanti quanti sono, dovrebbero essere limitati. Se i molti sono, le cose che esistono sono infinite: infatti sempre in mezzo alle cose che sono cene sono altre, ed altre ancora in mezzo a queste. E così le cose esistenti sono infinite». Poiché non sempre tra due cose se ne deve ammettere una terza, in quanto possono esistere collezioni di cose discrete e finite, anche in questo caso si è pensato che il ragionamento zenoniano si applichi solo a insiemi densi, come quelli dei punti, tra due dei quali è sempre possibile inserirne un terzo. Ma anche in questo caso è molto più probabile che Zenone, anziché far riferimento a qualcosa come il 'continuo' o lo 'spazio euclideo', partisse da processi intuitivi, quali l'inserimento di un intervallo tra due corpi, e supponesse l'esecuzione di un'operazione simile all'interno di un corpo per dividerne le parti.
Secondo Diogene Laerzio, Zenone argomentava anche contro il movimento sostenendo che «ciò che si muove non si muove né nel luogo in cui è, né in quello in cui non è». Per Aristotele quattro sono i ragionamenti di Zenone intorno al movimento.
Il primo argomento contro il moto, detto la dicotomia, parte dalla considerazione che un mobile non può mai arrivare al termine della traiettoria, perché prima di percorrere il percorso intero deve percorrerne la metà. Questo testo è stato variamente inteso. (Fig 1)
A). Dato il percorso A-B, prima di giungere in B, il mobile deve percorrere ½(A-B), raggiungendo A1, ma prima di raggiungere A1, deve percorrere 3/2(A-A1) e così via.

B). Supposto che il mobile abbia raggiunto il punto A1, a metà del percorso A-B, esso dovrà percorrere ½ (A2-B) prima di raggiungere B, e poi 1/2(A2-B) e così via.
Aristotele spiegava la difficoltà posta da questo argomento dicendo che in esso una traiettoria infinita doveva essere percorsa in un tempo finito. In entrambe le interpretazioni il mobile dovrà percorrere infiniti intervalli decrescenti di 1/2, 1/4, 1/8,..., dove il denominatore potrà crescere all'infinito.
Il secondo argomento contro il moto è quello detto di Achille o di Achille e la tartaruga. Si supponga che Achille insegua una tartaruga, che ha su di lui un vantaggio iniziale; pur muovendosi con una velocità maggiore di quella della tartaruga, Achille non la raggiungerà mai, perché, se si suppone che AB sia il vantaggio della tartaruga su Achille, questi deve giungere in B, per raggiungere la tartaruga.Nel frattempo però la tartaruga sarà passata in A1 e, quando Achille sarà giunto in A1, essa sarà ìn A2 e così via.

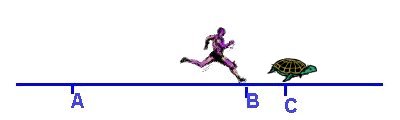
Secondo Aristotele questo argomento era identico al precedente, con la sola differenza che qui non si ha una serie di dimezzamenti, ma gli spazi che dividono Achille dalla tartaruga diventano sempre più piccoli secondo la serie 1/n, 1/n2 , 1/n3... . <br />
Il terzo argomento contro il moto e quello detto della freccia. In ogni momento dato un corpo occupa uno spazio esattamente uguale alla sua grandezza, e quando un corpo occupa uno spazio uguale a se stesso è in quiete. Pertanto in ogni istante di un movimento il mobile sarà in quiete, e un movimento non può risultare da una somma di stati di quiete.
II quarto argomento contro il moto, detto anche delle masse nello stadio, suppone che in uno stadio ci siano tre serie (A1, A2, A3, A4; B1, B2, B3, B4; C1, C2, C3, C4) di corpi. Le tre serie hanno uguale lunghezza e una (A1-A4) è ferma, mentre le altre due si muovono con la stessa velocità lungo percorsi paralleli. Una serie si muove dall'estremità dello stadio e l'altra in senso inverso dalla metà dello stadio verso quell'estremità. Nella posizione iniziale B3 e B4 sono in corrispondenza di A1 e A2, mentre C1 e C2 sono in corrispondenza di A3 e A4. (Fig 2a)

La serie delle C si è gia mossa verso sinistra perchè al tempo zero C1,C2 sono in corrispondenza di A3,A4

Ci dovrebbe essere un momento in cui ciascuna massa di una serie sarà allineata con la massa corrispondente delle altre due serie, sicché gli estremi A1-B1-C1 e A4-B4-C4 combaceranno. (Fig. 2b) Per raggiungere questa disposizione le masse B e C superano le une rispetto alle altre di 4 intervalli, perché B4 nella posizione iniziale non corrisponde a nessun C, mentre nella posizione finale corrisponde a C4: dunque i B e i C sono sfilati gli uni rispetto agli altri di 4 posizioni. Ma nello stesso tempo, B4 raggiunge A4 e C1 raggiunge A1 muovendosi di 2 soli intervalli. Poiché le serie sono tutte uguali, bisogna ammettere che i corpi in movimento hanno percorso nello stesso tempo spazi uguali e diseguali. Potrebbe essere Aristotele che, esponendo l'argomento della freccia, attribuisce a Zenone la concezione del tempo come somma di istanti in ognuno dei quali la freccia è stazionaria. E Aristotele liquida anche l'argomento delle masse nello stadio con l'osservazione che Zenone trascura le velocità relative dei mobili. La critica aristotelica potrebbe dipendere dal fatto che Aristotele espone gli argomenti zenoniani riferendoli a intervalli finiti e a corpi macroscopici di grandezza finita. Non così faceva con i primi due argomenti contro il moto, la dicotomia e Achille, esponendo i quali sosteneva che Zenone fa percorrere distanze infinite in tempi finiti. In effetti Aristotele faceva riferimento a Zenone nel trattare di infinito e di continuo, e la letteratura filosofica e matematica posteriore ha ripreso quelle argomentazioni.
Quando nell'Ottocento si sistemò la teoria matematica del continuo, parve che anche i paradossi zenoniani potessero esser spiegati e risolti. Nacque così una storiografia che presentava le argomentazioni zenoniane in chiave matematica, tanto più che si poteva pensare che Zenone facesse riferimento a una matematica pitagorica entrata in crisi con la scoperta delle grandezze incommensurabili; e con quella crisi Zenone poteva esser collegato, perché i suoi paradossi nascevano dalla scoperta del continuo, che solo la moderna teoria degli insiemi rendeva possibile padroneggiare.
La storiografia più recente ha cercato di liberarsi dalla prospettiva matematica. La matematica pitagorica è apparsa un'improbabile invenzione, e gli storici sono diventati prudenti nell'introdurre riferimenti all'infinito nei paradossi di Zenone; hanno invece preferito ricostruire il suo linguaggio filosofìco, nel quale i problemi dell'infinito matematico e del continuo non sono presenti.
Non è escluso che Zenone fosse diventato un personaggio al quale si potevano assai liberamente attribuire argomenti paradossali, come quel sorite con il quale avrebbe sostenuto che ogni grano di miglio dovrebbe far rumore cadendo, se fa rumore tutto il mucchio. Oggi è difficile farci un'idea del tipo di scritti nei quali erano esposti i 'paradossi' di Zenone, del pubblico al quale si rivolgevano, della funzione che dovevano compiere.
Spesso tra i rappresentanti della filosofia presocratica si cita Epicarmo, un personaggio vissuto tra la fine del VI e il V secolo a.C., al quale veniva attribuita l'invenzione della commedia. Alcimo accusò Platone di aver trovato in Epicarmo molte cose e di averle copiate, e la tradizione pitagorica s'impadronì di lui, facendone uno scolaro di Pitagora. Tutte queste notizie sono poco attendibili. E' certo che Epicarmo era un rappresentante della vita intellettuale delle colonie greche dell'Italia meridionale e della Sicilia, e che scrisse delle composizioni teatrali.In esse compaiono argomentazioni 'di tipo filosofìco'. Trattandosi di dialoghi non c'è da stupirsi che Epicarmo mettesse in scena dottrine che potevano colpire per la loro stranezza e che potevano essere attribuite ai personaggi rappresentati.
Proprio gli eleati diventeranno popolari per la paradossalità delle loro tesi. Ma i testi di Epicarmo potrebbero anche rivelare modi di argomentare inconsueti, e tuttavia diffusi nella cultura letteraria e codificati nella cosiddetta cultura fìlosofica.E possibile trovarvi versi che ricordano Senofane, che possono far venire in mente i paradossi zenoniani e che avranno echi ancora nel Fedone di Platone. Tutto questo non autorizza a dire che Epicarmo sia una fonte di Platone, così come non è possibile dire che ci siano stati rapporti tra Epicarmo e Senofane, Parmenide o Zenone. Ma il riferimento a Epicarmo può mostrare che certi modi di ragionare sono nati proprio nel linguaggio letterario e nella sua ricerca della sottigliezza e del paradosso.Tutto sommato, forse Zenone non ha dato voce a una teoria dell'infinito o del continuo o dello spazio geometrico, ma ha semplicemente costruito paradossi assumendo che una cosa non coincida con la somma delle sue parti, che un movimento sia una somma di stati stazionari, che prima di esser giunti a una posizione bisogna aver occupato la posizione precedente e così via. In questo senso egli riprendeva un elemento parmenideo. Parmenide aveva sostenuto che, una volta introdotta, la negazione genera parole, ciascuna delle quali pretende di avere un riferimento autonomo: e nasce un'immagine fallace dell'universo. Zenone fa qualcosa di analogo: se si mette una parte tra altre due o una tappa prima di un termine, non si può poi più ricostituire il tutto.
La fortuna di Zenone nella letteratura retorica e sofistica fa supporre che la sua connessione con la logica, la dialettica e la matematica possa essere molto sviante. I filologi hanno riportato le arditezze speculative dell'eleatismo al linguaggio letterario arcaico e gli storici della filosofìa hanno cercato di trovare negli usi del linguaggio comune le fonti dei paradossi di Zenone.Queste impostazioni sono in parte figlie della moda filosofica del nostro tempo. Ma certamente non conviene cercare in Zenone un critico della matematica pitagorica o un protagonista della nascita della matematica greca classica o uno scopritore delle difficoltà che la teoria moderna degli insiemi avrebbe risolto.
Zenone è rimasto una figura popolare nella nostra tradizione, e filosofi e matematici moderni hanno spesso fatto riferimento a lui; ma l'immagine che ne è sopravvissuta, passata attraverso i testi aristotelici e legata alla teoria aristotelica dell'infinito e del continuo, si è formata all'interno dei gruppi platonici nel corso della discussione sulla matematica e il movimento.In quel momento la matematica offriva una teoria della molteplicità e del movimento che poteva costituire una difficoltà per le teorie filosofiche condivise dai platonici. Dovette nascere l'idea che le difficoltà filosofiche generate da quelle teorie matematiche dipendessero dall'infinito, e i paradossi di Zenone dovettero sembrare la prova più eloquente in proposito. Infatti, prima di Platone, Zenone è conosciuto soprattutto come costruttore di paradossi e lo stesso Platone partiva da questa immagine per fare di lui un semplice difensore della filosofia parmenidea.Poi, forse già Platone, ma certamente Aristotele si servirono delle argomentazioni di Zenone per mostrare le difficoltà alle quali va incontro il tentativo di introdurre l'infinito.
OPERE
Anche per quel che riguarda l'opera di Zenone la notizia più antica è quella di Platone (Parmenide), che parla di uno scritto di Zenone, che allora arrivava per la prima volta ad Atene. Una tradizione attribuiva a Zenone più opere, forse quattro (Dispute, Esame delle dottrine di Empedocle, Contro i filosofi e Sulla natura),ma gli storici hanno riconosciuto in questi titoli tutt'al più il riferimento tardo a parti di una stessa opera.
Non sappiamo molto della struttura dello scritto di Zenone. Platone parla dei «discorsi» che lo componevano e sembra riconoscere in ogni discorso più «ipotesi». Probabilmente nel gruppo platonico era invalsa l'abitudine di rappresentare gli eleati, a cominciare dallo stesso Parmenide, nell'atto di discutere. Proclo attribuiva a Zenone ben quaranta argomenti, mentre ai quaranta argomenti contro la molteplicità Elia aggiungeva cinque ragionamenti contro il moto. Per noi è difficile accedere direttamente allo scritto di Zenone, perduto. Aristotele cita ampiamente argomentazioni zenoniane; ma non sappiamo affatto se egli attinga fedelmente a qualche scritto o se le sue siano interpretazioni di argomentazioni di Zenone o che si facevano risalire a Zenone.

RIASSUMENDO

Paradossi contro il pluralismo

Primo paradosso 

Il primo paradosso, contro la pluralità delle cose, sostiene che se le cose sono molte esse sono allo stesso tempo un numero finito e un numero infinito: sono finite in quanto esse sono né più né meno di quante sono, e infinite poiché tra la prima e la seconda ce n'è una terza e così via.

Secondo paradosso

Il secondo paradosso invece sostiene che se queste unità non hanno grandezza, le cose da esse composte non avranno grandezza, mentre se le unità hanno una certa grandezza, le cose composte da infinite unità avranno una grandezza infinita.

Paradossi contro il movimento

Primo paradosso (lo stadio - unità di misura della lunghezza pari a 177,6 m.)

Il primo argomento contro il movimento è quello sullo stadio.

Esso afferma che non si può giungere all'estremità di uno stadio senza prima aver raggiunto la metà di esso, ma prima di raggiungerla si dovrà raggiungere la metà della metà e così via senza quindi mai riuscire a raggiungere l'estremità dello stadio.

Secondo paradosso (Achille e la tartaruga)

Il Paradosso di Achille e la tartaruga - uno dei paradossi di Zenone più famosi - afferma invece che se Achille venisse sfidato da una tartaruga  nella corsa e concedesse alla tartaruga un piede di vantaggio, egli non riuscirebbe mai a raggiungerla, dato che Achille dovrebbe prima raggiungere la posizione occupata precedentemente dalla tartaruga che, nel frattempo, sarà avanzata raggiungendo una nuova posizione che la farà essere ancora in vantaggio; quando poi Achille raggiungerà quella posizione nuovamente la tartaruga sarà avanzata precedendolo ancora. Questo stesso discorso si può ripetere per tutte le posizioni successivamente occupate dalla tartaruga e così la distanza tra Achille e la tartaruga pur riducendosi verso l'infinitamente piccolo non arriverà mai ad essere pari a zero.

In pratica, posto che la velocità di Achille (Va) sia N volte quella della tartaruga (Vt) le cose avvengono così:

• dopo un certo tempo t1 Achille arriva dove era la tartaruga alla partenza (L1).
• nel frattempo la tartaruga ha compiuto un pezzo di strada e si trova nel punto L2.
• occorre un ulteriore tempo t2 per giungere in L2.
• ma nel frattempo la tartaruga è giunta nel punto L3 ... e così via.

Quindi per raggiungere la tartaruga Achille impiega un tempo

e quindi non la raggiungerà mai.

Terzo paradosso (la freccia)

Il terzo argomento è quello della freccia, che appare in movimento ma, in realtà, è immobile. In ogni istante difatti essa occuperà solo uno spazio che è pari a quello della sua lunghezza; e poiché il tempo  in cui la freccia si muove è fatto di singoli istanti, essa sarà immobile in ognuno di essi.

Il concetto di questo terzo paradosso è in fondo opposto a quello del secondo: l'esistenza di punti e istanti indivisibili. Ma anche in questo caso il movimento risulta impossibile, in quanto dalla somma di istanti immobili non può risultare un movimento.

Quarto paradosso (due masse nello stadio) 

Zenone afferma che se due masse in uno stadio si vengono incontro, risulterà l'assurdo logico  che la metà del tempo equivale al doppio.

Consideriamo infatti tre segmenti (A, B, C) uguali e paralleli, che si trovino allineati. Supponiamo poi che il segmento in alto (A) si muova verso destra, rispetto a quello situato nel centro (B) che resta fermo, e che per ogni istante elementare avanzi di un intervallo (elementare). Il segmento in basso (C) faccia invece la stessa cosa verso sinistra. Dopo il primo istante avremo che i punti iniziali di A e C si saranno allontanati di due intervalli. Ma ciò è assurdo perché allora il tempo che avrebbero impiegato per allontanarsi di un solo intervallo sarebbe di "mezzo istante", contraddicendo l'ipotesi che stiamo analizzando la situazione al primo istante (indivisibile).

Confutazione dei paradossi del moto

In alcuni dei suoi paradossi, Zenone assume implicitamente che, data una serie  infinita, debba essere infinita anche la sua somma.

Nel caso specifico di Achille e della tartaruga la serie dei tempi ti converge e

Non crediamo però che l'errore sia "sciocco": una prima dimostrazione di convergenza delle serie infinite non geometriche è stata data, nel solo caso particolare di

solo nel XIV secolo da Richard Suiseth.

Il caso generale venne dimostrato nel XVII secolo, mentre Zenone espose i suoi paradossi nel V secolo a.C. La tecnica mostrata da Zenone nella suddivisione infinitesimale va sotto il nome di dicotomia.

Il paradosso della freccia, come quello dello stadio, possono essere confutati sviluppando una teoria dei numeri reali che permetta di postulare che lo spazio e il tempo siano infinitamente divisibili, e definendo al contempo la possibilità di misurare un insieme di cardinalità illimitata, concetti che sono stati resi formalmente solo alla fine del XIX secolo.

Nel paradosso delle masse dello stadio, Zenone implicitamente suppone che le velocità possibili di un corpo siano illimitate superiormente, mentre sappiamo dalla  teoria della relatività ristretta che non è così. Anche in quello della freccia, egli suppone che un corpo in moto sia indistinguibile da uno in quiete. Sono trascorsi 2500 anni prima di raggiungere le conoscenze necessarie a confutare il paradosso.

Sono state date anche delle confutazioni valide anche per la meccanica classica. In genere si è sempre osservato che gli argomenti di Zenone si basano sull'infinito. Per il paradosso della freccia, Bertrand Russell ha osservato che il cinematografo crea il movimento utilizzando una successione di immagini ferme.

Esiste un'altra visione dei paradossi di Zenone: un atto "semplice" viene scomposto e descritto attraverso una successione infinita di atti.

Effetto Zenone quantistico

Come si può vedere, questi paradossi sono stati utili per sviluppare molti concetti alla base della matematica e della fisica moderne, e non si dovrebbe liquidarli banalmente. Persino nella meccanica quantistica riecheggia il nome di Zenone nel cosiddetto "effetto Zenone quantistico", che, riprendendo metaforicamente il paradosso della freccia, afferma che un sistema, che decadrebbe spontaneamente, è inibito o addirittura non decade affatto se sottoposto ad una serie infinita di osservazioni (o misure). Di recente vari esperimenti: - l'esperimento di Itano et al. (1990), basatosi sull'idea di Cook (1988), - quello di Kwiat et al. (1995) sulla polarizzazione dei fotoni, - e quello di Fischer et al. (2001), hanno dato verifica sperimentale di questo effetto.

Un primo tentativo di confutazione dei paradossi di Zenone è ascrivibile ad Aristotele, che notava come i paradossi si basassero sull’infinita divisibilità del tempo. Aristotele concludeva ipotizzando che il tempo invece non è mai infinitamente divisibile (istanti discreti). Da ciò ne derivava la logica conseguenza che istanti finiti permettessero di colmare spazi infinitamente discreti. Le osservazioni di Aristotele, che implicano una radicale differenza qualitativa tra tempo e spazio, verranno riprese da Bergson, che nei suoi studi sulla durata dimostra che i filosofi e gli scienziati, applicando divisioni numeriche, analizzano il tempo come fosse lo spazio. Per Bergson tempo e spazio, invece, appartengono ad ambiti qualitativi differenti che l’analisi numerica, per via della oggettiva comodità dei suoi risultati, tende a far ignorare. Per Bergson il tempo ha una natura qualitativa che è differente a seconda della natura di ciascun oggetto esaminato. Il tempo in cui si scioglie una zolletta di zucchero, per fare un esempio banale, sarà differente da quello in cui si scioglie la medesima quantità di miele. Da ciò ne deduceva che esiste una precisa durata qualitativa differente a seconda della natura delle cose. Partendo da questo presupposto è chiaro che la qualità del tempo della tartaruga è radicalmente differente da quella di Achille. Posto anche che lo spazio che divide Achille dalla tartaruga sia fatto di infinite porzioni di spazio (ma in realtà la fisica ha mostrato come spazio e tempo siano strettamente correlati) come immaginava Zenone, la qualità del tempo in cui si muove Achille è radicalmente differente (ad esempio è differente la sua velocità da quella della tartaruga) e incrementa lo spazio percorso in ogni istante. Se la seconda in un istante y percorre uno spazio uguale a x, possiamo immaginare che la velocità di Achille sia tale che in ogni istante y percorra uno spazio che sia il quadrato dello spazio percorso nell’istante precedente e poi il cubo e così via, salendo ogni volta di potenza. In altri termini, se il movimento della tartaruga è esprimibile con una sommatoria induttiva alla Peano (1+1+1+…n+k) all’infinito, il movimento di Achille è esprimibile come una somma di potenze (2²+ 2³ + 2esp4 +… 2espn+2espk) all’infinito. Pertanto Achille raggiunge la tartaruga perché le due progressioni infinite sono qualitativamente differenti.

VIDEO 1: https://www.youtube.com/watch?v=CQ-Tk6pR4Wg

VIDEO 2: https://www.youtube.com/watch?v=Sw4WiwASGAs

Eugenio Caruso - 30 maggio 2020

Tratto da