Leonardo Fibonacci, uno dei matematici più famosi di tutti i tempi.

Leonardo Pisano detto Fibonacci (Pisa, settembre 1170 circa – Pisa, 1242 circa) è considerato uno dei più grandi matematici di tutti i tempi. Con altri dell'epoca contribuì alla rinascita delle scienze esatte dopo la decadenza dell'età tardo-antica e dell'Alto Medioevo. Con lui, in Europa, ci fu l'unione fra i procedimenti della geometria greca euclidea (gli Elementi) e gli strumenti matematici di calcolo elaborati dalla scienza araba (in particolare egli studiò per la parte algebrica il Liber embadorum dello studioso ebreo spagnolo Abraham ibn 'Ezra).
I dati della sua biografia sono scarsi e confusi, e desumibili in gran parte da notizie contenute nelle sue opere, oltre che da due documenti d'archivio. In particolare non sono note né la data di nascita, né quella di morte, collocabili la prima nel decennio 1170-1180 e la seconda dopo il 1241.
Assieme al padre Guglielmo dei Bonacci, facoltoso mercante pisano e rappresentante dei mercanti della Repubblica di Pisa (nell'epistola di dedica a Michele Scoto si legge che il padre era publicus scriba pro pisanis mercatoribus) nella zona di Bugia in Algeria, passò alcuni anni in quella città, dove studiò i procedimenti aritmetici che studiosi musulmani stavano diffondendo nelle varie parti del mondo arabo. Qui ebbe anche precoci contatti con il mondo dei mercanti e apprese tecniche matematiche sconosciute in Occidente. Alcuni di tali procedimenti erano stati introdotti per la prima volta dagli indiani, portatori di una cultura diversa da quella occidentale. Proprio per perfezionare queste conoscenze Fibonacci viaggiò molto in Egitto, Siria, Sicilia, Grecia arrivando a Costantinopoli, alternando presumibilmente il commercio con gli studi matematici. Molto dovette ai trattati di Mu?ammad ibn Musa al-Khwarizmi, di Abu Kamil e al confronto con i maestri arabi, senza però essere mero diffusore della loro opera. Ritornato in Italia, la sua notorietà giunse anche alla corte dell'imperatore Federico II. Il matematico e l'imperatore si incontreranno a Pisa, presumibilmente nell'estate del 1226.
La Repubblica di Pisa gli assegnò un vitalizio che gli permise di dedicarsi completamente ai suoi studi: «Considerando l’onore e il profitto della nostra città e dei cittadini, che derivano loro dalla dottrina e dai diligenti servigi del discreto e sapiente maestro Leonardo Bigollo nelle stime e ragioni d’abaco necessarie alla città e ai suoi funzionari, e in altre cose quando occorre, deliberiamo col presente atto che allo stesso Leonardo, per la sua dedizione e scienza e in ricompensa del lavoro che sostiene per studiare e determinare le stime e le ragioni sopraddette, vengano assegnate dal comune e dal tesoro pubblico venti lire a titolo di mercede o salario annuo, oltre ai consueti benefici, e che inoltre lo stesso [Leonardo] serva come al solito il comune pisano e i suoi funzionari nelle pratiche d’abaco».
Nel documento si legge che Fibonacci era detto “Bigollo” (“Discretus et sapiens magister Leonardo Bigollo”), epiteto che in passato si riteneva essere offensivo, ma che in realtà potrebbe significare “bilingue”, oppure “viaggiatore”. Come osserva Pier Daniele Napolitani: «La delibera si trova nel Constitutum pisanum legis et usus, conservato all’Archivio di Stato di Pisa ed è inserita nel volume del 1233 tra le aggiunte datate 1242; le date sono in stile pisano e corrispondono alle nostre 1233 e 1241. Il documento non è datato e quindi può essere relativo a uno qualsiasi degli anni compresi tra questi due. Il 1241 è quindi il limite temporale estremo oltre il quale non si hanno più notizie di Leonardo.». Il fatto che il Comune lo incaricasse della tenuta dei bilanci e dell'assistenza ai suoi funzionari nel corso degli anni Trenta spinge a formulare l'ipotesi che la sua nascita debba essere collocata più avanti del 1170 tradizionalmente accettato. A lui Pisa ha intitolato il lungarno che va dal Ponte alla Vittoria al Ponte della Fortezza.

Opere
Fibonacci è noto soprattutto per la sequenza di numeri da lui individuata e conosciuta, appunto, come "successione di Fibonacci" - 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 ... - in cui ogni termine, a parte i primi due, è la somma dei due che lo precedono. Sembra che questa sequenza sia presente in diverse forme naturali (per esempio, negli sviluppi delle spirali delle conchiglie). Una particolarità della sequenza o successione di Fibonacci è che il rapporto fra le coppie di termini successivi tende molto rapidamente al numero 1,61803..., noto con il nome di rapporto aureo o sezione aurea.

A Leonardo Fibonacci si devono:
il Liber abbaci, di argomento aritmetico e dedicato a Michele Scoto;
la Practica geometriae, con l'applicazione dell'algebra alla soluzione di problemi geometrici;
il Liber quadratorum, di argomento algebrico e dedicato a Federico II;
l'Epistola ad magistrum Theodorum, di breve estensione;
il Flos Leonardi Bigolli Pisani super solutionibus quarundam questionibus ad numerum et ad geometriam, vel ad utrumque pertinentium, dedicato a Raniero Capocci di Viterbo, cardinale diacono.
Pare, inoltre, che egli abbia composto anche due trattati andati perduti, uno dei quali potrebbe aver avuto il titolo di Liber minoris guise, o più semplicemente De minore guisa, mentre l'altro doveva essere un commento al libro X degli Elementi di Euclide.

Le sue opere potrebbero aver ispirato il disegno architettonico della porta di Capua ovvero quello del federiciano Castel del Monte. Inoltre i suoi studi furono così importanti che tutt'oggi esiste una pubblicazione periodica dedicata interamente alla sequenza aritmetica da lui elaborata, il Fibonacci Quarterly. Al matematico è stato anche dedicato l'asteroide 6765 Fibonacci.
Nel 1202 e poi successivamente nel 1228 Leonardo Fibonacci pubblicò il Liber abbaci, opera in quindici capitoli con la quale introdusse le nove cifre da lui definite "indiane", e il segno 0 (gli altri popoli non utilizzavano questo simbolo perché non ne sentivano il bisogno) che in latino è chiamato zephirus, adattamento dell'arabo sifr, ripreso a sua volta dal termine sanscrito sunya, che significa "vuoto". Zephirus in veneziano divenne zevero ed infine comparve l'italiano "zero". Per mostrare ad oculum l'utilità del nuovo sistema numerico, egli pose sotto gli occhi del lettore una tabella comparativa di numeri scritti nei due sistemi romano e indiano. Fibonacci espose così per la prima volta in Europa la numerazione posizionale indiana, così come l'aveva appresa dai matematici arabi (tale numerazione era stata infatti adottata dagli arabi).
Nel libro presentò inoltre criteri di divisibilità, regole di calcolo di radicali quadratici e cubici ed altro. Introdusse con poco successo anche la barretta delle frazioni, nota al mondo arabo prima di lui. Nel Liber abbaci sono anche compresi i quesiti matematici che gli furono posti dagli intellettuali del tempo, con la loro soluzione (uno dei capitoli trattava aritmetica commerciale, ragioneria, problemi di cambi, ecc.).
All'epoca il mondo occidentale usava i numeri romani e il sistema di numerazione greco, i calcoli si eseguivano con l'abaco. Il nuovo sistema introdotto da Fibonacci stentò molto ad essere accettato, tanto che nel 1280 la città di Firenze proibì l'uso delle cifre indo-arabe da parte dei banchieri, alcuni dei quali pare falsificassero lo zero a loro vantaggio, modificandolo in 6, 8 o 9. Da allora infatti lo zero, invece che a "cerchio" fu rappresentato ad "uovo" in modo da impedirne la falsificazione. Si riteneva inoltre che lo "0" apportasse confusione e venisse impiegato anche per mandare messaggi segreti e, poiché questo sistema di numerazione veniva chiamato "cifra", da tale denominazione deriva l'espressione "messaggio cifrato".
L'uso delle cifre arabe era in ogni caso già conosciuto da alcuni dotti dell'epoca. Il primo caso del quale si ha notizia è stato quello del monaco Gerberto (poi diventato papa dal 999 al 1003 col nome di Silvestro II): egli propose l'uso di questo sistema in alcuni conventi in cui si scrivevano opere scientifiche, ma il metodo rimase sconosciuto nel mondo esterno. Un esempio più tardo, dell'epoca di Fibonacci si trova nelle scritture notarili di Notar Raniero, perugino. La prima edizione del Liber abbaci, del 1202, è andata persa, mentre la seconda edizione del 1228, che Fibonacci aveva preparato su richiesta del filosofo scozzese Michele Scoto, si è conservata in numerosi manoscritti ed è stata ristampata nel 1857 a Roma dalla Tipografia delle scienze matematiche e fisiche, in un'edizione curata da Baldassarre Boncompagni.

La successione di Fibonacci (detta anche successione aurea), indicata con {F{n}}o con {Fib(n)}, in matematica indica una successione di numeri interi in cui ciascun numero è la somma dei due precedenti, eccetto i primi due che sono, per definizione: F{0}=0 e F{1}=1. Questa successione è definita ricorsivamente secondo la seguente regola:

F{0}=0

F{1}=1

F{n}=F{n-1}+F{n-2}} (per ogni n>1)

Gli elementi F{n} sono anche detti numeri di Fibonacci. I primi termini della successione di Fibonacci sono:  0,1,1,2,3,5,8,13,21,34,55,89,144,233,

L'intento di Leonardo Fibonacci era quello di trovare una legge matematica che descrivesse la crescita di una popolazione di conigli.

Assumendo per ipotesi che:

• si disponga di una coppia di conigli appena nati
• questa prima coppia diventi fertile al compimento del primo mese e dia alla luce una nuova coppia al compimento del secondo mese;
• le nuove coppie nate si comportino in modo analogo;
• le coppie fertili dal secondo mese di vita in poi diano alla luce una coppia di figli al mese;

si verifica quanto segue:

• dopo un mese una coppia di conigli sarà fertile,
• dopo due mesi ci saranno due coppie di cui una sola fertile,
• nel mese seguente, terzo mese dal momento iniziale, ci saranno 2+1=3 coppie perché solo la coppia fertile avrà generato; di queste tre, due saranno le coppie fertili, quindi
• nel mese seguente (quarto mese dal momento iniziale) ci saranno  3+2=5 coppie

In questo esempio, il numero di coppie di conigli di ogni mese esprime la successione di Fibonacci.

Il rapporto  F{n}/F{n - 1}, per n tendente all'infinito, tende al numero algebrico irrazionale phi, chiamato sezione aurea o numero di Fidia. In termini matematici:

lim {per n tendente all'infinito}F{n} / F{n-1}=phi

 

con semplici passaggi algebrici si dimostra che:

phi =(1+5^1/2)/ 2=1,6180339887 ......

Numeri di Fibonacci e legami con altri settori
In matematica i numeri di Fibonacci sono legati in qualche modo alla sezione aurea, alla sequenza di Farey, alle frazioni continue, alla zeta di Fibonacci, alla zeta di Riemann, ai gruppi di Lie, ai frattali.
In Fisica sussiste il legame con la teoria delle stringhe. Molti altri legami sono evidenti con la biologia, la cristallografia, la musica, l'economia, l'arte, l'elettrotecnica, l'informatica, ecc. Tuttavia non mancano esempi di "avvistamenti" della successione di Fibonacci un po' forzati: lo rivelano Gael Mariani e Martin Scott dell'Università di Warwick, con un articolo su New Scientist del settembre 2005.

Nella musica
La musica ha numerosi legami con la matematica, e molti ritengono che importante sia in essa il ruolo della sezione aurea e dei numeri di Fibonacci. Sul piano compositivo, attraverso la successione di Fibonacci la sezione aurea può essere rapportata a qualsiasi unità di misura concernente la musica, cioè durata temporale di un brano, numero di note o di battute, etc. Anche se vi sono stati fraintendimenti numerici: nel 1978, per esempio, nei Kyrie contenuti nel Liber Usualis Paul Larson riscontrò il rapporto aureo a livello delle proporzioni melodiche, ma in mancanza di una documentazione che ne attesti un'effettiva volontà di inserimento, la non casualità della ricorrenza rimane tutta a livello puramente congetturale. Simili illazioni sono più volte state espresse circa le opere di Mozart, anche se recentemente John Putz, matematico all'Alma College, convinto anche lui di tale teoria (specialmente per quanto riguarda le sue sonate per pianoforte), dovette ricredersi riscontrando un risultato decente soltanto per la Sonata n. 1 in Do maggiore. I musicologi hanno trovato altre applicazioni nei rapporti fra le durate (in misure) delle varie parti dei brani musicali, in particolare si trovano questi rapporti nelle opere di Claude Debussy e di Béla Bartók. Tra i compositori del XX secolo si evidenziano in proposito Stravinsky, Xenakis, Stockhausen (nel cui brano Klavierstücke IX si hanno frequenti rimandi alle successioni fibonacciane nelle segnature di tempo), Luigi Nono, Ligeti, Giacomo Manzoni e Sofija Asgatovna Gubajdulina che disse a proposito di Bartok: «[...] L'aspetto ritmico della musica di Bartók mi interessa moltissimo, al punto che vorrei studiare a fondo la sua applicazione della Sezione Aurea.» Tuttavia è molto difficile stabilire se l'artista abbia voluto consciamente strutturare l'opera con la sezione aurea o se questa non sia piuttosto frutto della sua sensibilità artistica, dato che la sezione aurea si riscontra spesso in natura (come ad esempio nelle stelle marine, in ammoniti, conchiglie, ananas, pigne e nella forma dell'uovo). Infatti, mentre alcuni ritengono che i sopra citati Debussy e Bartok abbiano deliberatamente impiegato la sezione aurea, per altri questo è meno scontato. D'altronde Debussy stesso scrisse esplicitamente al suo editore Durand (nell'agosto 1903): (FR) «Vous verrez, à la page 8 de "Jardins sous la Pluie", qu'il manque une mesure; c'est d'ailleurs un oubli de ma part, car elle n'est pas dans le manuscrit. Pourtant, elle est nécessaire, quant au nombre; le divine nombre [...].». «Lei vedrà, alla pagina 8 di "Jardins sous la Pluie" che manca una battuta; è del resto una mia dimenticanza, perché non è nel manoscritto. Eppure, è necessaria, per il numero; il divino numero [...].» Nel Novecento le avanguardie della musica colta e molti tra gli eredi del serialismo, come i già citati Karlheinz Stockhausen, György Ligeti e Iannis Xenakis, applicarono invece sistematicamente e intenzionalmente - a differenza della maggioranza dei loro predecessori - i numeri di Fibonacci alla musica, approfondendone lo studio e la conoscenza; facendo evolvere i precedenti utilizzi della matematica in musica, hanno introdotto un utilizzo più strutturato della matematica (soprattutto il calcolo delle probabilità e del computer per la composizione musicale). Xenakis in particolare ha fondato a tale fine, a Parigi nel 1972, un gruppo di ricerca universitario chiamato CEMAMU, che ha appunto come obiettivo l'applicazione delle conoscenze scientifiche moderne e del computer alla composizione musicale e alla creazione di nuovi suoni tramite sintetizzatori. Anche la musica rock, specialmente nel cosiddetto rock progressivo, si è confrontata con gli aspetti mistico-esoterici della sezione aurea, e più precisamente dalla successione di Fibonacci. L'esempio più emblematico è la musica dei Genesis, che hanno usato assiduamente questa successione nella costruzione armonico-temporale dei loro brani; Firth of Fifth è tutto basato su numeri aurei: ad esempio ci sono assoli di 55, 34, 13 battute, di questi alcuni sono formati da 144 note, etc. Oltre ai Genesis, altre rock band hanno usato, seppure più sporadicamente, i numeri aurei nelle loro composizioni. Fra questi i Deep Purple nel brano Child in Time e i Dream Theater nell'album Octavarium, interamente concepito secondo il rapporto tra i numeri 8 e 5 e termini consecutivi della sequenza di Fibonacci. Risale invece al 2001 Lateralus album della band statunitense Tool che contiene il singolo omonimo "Lateralus" costruito fedelmente sulla successione di Fibonacci: i Tool fanno un sapiente uso dei primi elementi della successione di Fibonacci: contando infatti le sillabe della prima strofa si ottiene 1,1,2,3,5,8,5,3,2,1,1,2,3,5,8,13,8,5,3. Inoltre la ritmica della canzone alterna battute da 9/8, 8/8 e 7/8, il numero ottenuto è 987 che è il sedicesimo numero della sequenza. Da notare che la canzone fa un continuo riferimento alla figura della spirale ([...] To swing on the spiral [...] Spiral out. Keep going [...]).

In botanica
Quasi tutti i fiori hanno tre o cinque o otto o tredici o ventuno o trentaquattro o cinquantacinque o ottantanove petali: ad esempio i gigli ne hanno tre, i ranuncoli cinque, il delphinium spesso ne ha otto, la calendula tredici, l'astro ventuno, e le margherite di solito ne hanno trentaquattro o cinquantacinque o ottantanove. I numeri di Fibonacci sono presenti anche in altre piante come il girasole; difatti i piccoli fiori al centro del girasole (che è in effetti una infiorescenza) sono disposti lungo due insiemi di spirali che girano rispettivamente in senso orario e antiorario. I pistilli sulle corolle dei fiori spesso si dispongono secondo uno schema preciso formato da spirali il cui numero corrisponde ad uno della successione di Fibonacci. Di solito le spirali orientate in senso orario sono trentaquattro mentre quelle orientate in senso antiorario cinquantacinque (due numeri di Fibonacci); altre volte sono rispettivamente cinquantacinque e ottantanove, o ottantanove e centoquarantaquattro. Si tratta sempre di numeri di Fibonacci consecutivi. I numeri di Fibonacci sono presenti anche nel numero di infiorescenze di ortaggi come il Broccolo romanesco. Le foglie sono disposte sui rami in modo tale da non coprirsi l'una con l'altra per permettere a ciascuna di esse di ricevere la luce del sole. Se prendiamo come punto di partenza la prima foglia di un ramo e contiamo quante foglie ci sono fino a quella perfettamente allineata, spesso questo numero è un numero di Fibonacci, e anche il numero di giri in senso orario o antiorario che si compiono per raggiungere tale foglia allineata dovrebbe essere un numero di Fibonacci. Il rapporto tra il numero di foglie e il numero di giri si chiama “rapporto fillotattico” (vedi Fillotassi).

La disposizione dei fiori nel capolino del girasole

Nel corpo umano
Il rapporto fra le lunghezze delle falangi del dito medio e anulare di un uomo adulto è aureo, come anche il rapporto tra la lunghezza del braccio e l'avambraccio, e tra la lunghezza della gamba e la sua parte inferiore.

In geometria e in natura
La spirale di Fibonacci, creata mediante l'unione di quadrati con i lati equivalenti ai numeri della successione di Fibonacci. Se si disegna un rettangolo con i lati in rapporto aureo fra di loro, lo si può dividere in un quadrato e un altro rettangolo, simile a quello grande nel senso che anche i suoi lati stanno fra loro nel rapporto aureo. A questo punto il rettangolo minore può essere diviso in un quadrato e un rettangolo che ha pure i lati in rapporto aureo, e così via.

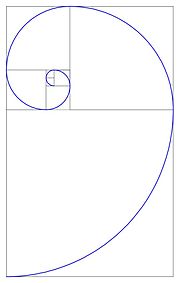
La spirale di Fibonacci, creata mediante l'unione di quadrati con i lati equivalenti ai numeri della successione di Fibonacci

La curva che passa per vertici consecutivi di questa successione di rettangoli è una spirale che troviamo spesso nelle conchiglie e nella disposizione dei semi del girasole e delle foglie su un ramo, oltre che negli alveari delle api.

In apicoltura
Leonardo da Pisa o Fibonacci visse vicino a Béjaïa, a quell'epoca importante città esportatrice di cera (da ciò deriva la versione francese del nome della città, "bougie", che significa "candela" in francese). Una recente analisi matematico-storica del periodo e della regione in cui visse Fibonacci suggerisce che, in realtà, furono gli apicoltori di Bejaia e le loro conoscenze sulla riproduzione delle api la fonte di ispirazione per la Successione di Fibonacci e non il più noto modello della riproduzione dei conigli.

Nell'arte
I numeri di Fibonacci sono stati usati in alcune opere d'arte. La facciata del Partenone è un classico esempio de sezione aurea. Secondo Pietro Armienti, docente all'Università di Pisa ed esperto di petrologia (scienza delle rocce), le geometrie presenti sulla facciata della chiesa pisana di San Nicola sarebbero un chiaro riferimento alla successione del matematico. Mario Merz li ha usati nell'installazione luminosa denominata Il volo dei numeri, su una delle fiancate della Mole Antonelliana di Torino. Sulle mura di San Casciano in Val di Pesa, inoltre, accanto ad un cervo imbalsamato, sono permanentemente installati i numeri al neon riportanti le cifre 55, 89, 144, 233, 377 e 610. Si tratta di una creazione di Merz realizzata in occasione della mostra Tuscia Electa del 1997. Lo stesso autore ha inoltre realizzato nel 1994 un'installazione permanente sulla ciminiera della compagnia elettrica Turku Energia a Turku, in Finlandia. Tutta l'opera di Tobia Ravà fa riferimento alla successione di Fibonacci, scoprendone anche una specifica proprietà. Anche il pittore austriaco Helmutt Bruck ha dipinto quadri omaggianti Fibonacci e prodotto opere in serie di 21. A Barcellona e a Napoli è stata creata un'installazione luminosa: nella città spagnola si trova nell'area della Barceloneta, all'interno dell'area pedonale, dove i numeri sono posti a distanze proporzionali alla loro differenza, mentre a Napoli sono disposti a spirale all'interno della stazione Vanvitelli della linea 1 della metropolitana, e più precisamente sul soffitto che sovrasta le scale mobili quando, superate le obliteratrici, si scende all'interno della stazione vera e propria. Nel 2017, ad Albissola Marina, nella Piazzetta Poggi del centro storico, è stato installato un mosaico pavimentale dal titolo Fiore di Fibonacci, dovuto all'artista Gabriele Gelatti.

Nell'economia
I numeri di Fibonacci sono utilizzati anche in economia nell'Analisi tecnica per le previsioni dell'andamento dei titoli in borsa, secondo la teoria delle onde di Elliott. Studiando i grafici storici dei titoli, Ralph Nelson Elliott sviluppò un metodo basato su tredici conformazioni grafiche dette onde, simili per forma ma non necessariamente per dimensione. A differenza di altre applicazioni grafiche come medie mobili, trendline, macd, rsi ecc. che si limitano ad indicare il livello di resistenza e di supporto e le angolature del trend "Il principio delle onde di Elliott" è l'unico metodo in grado di individuare un movimento del mercato dall'inizio alla fine e quindi di presumere i futuri andamenti dei prezzi.

In informatica
I numeri di Fibonacci sono utilizzati anche nel sistema informatico di molti computer. In particolare vi è un complesso meccanismo basato su tali numeri, detto "Fibonacci heap" che viene utilizzato nel processore Pentium della Intel per la risoluzione di particolari algoritmi. In elettrotecnica Una rete di resistori, ad esempio un Ladder Network (Rete a scala), ha una resistenza equivalente ai morsetti A e B esprimibile sia come frazione continua che tramite la sezione aurea o i numeri di Fibonacci.

Nei giochi sistemici
In qualunque gioco sistemico come totocalcio, superenalotto o roulette i numeri di Fibonacci possono essere utilizzati come montanti per le puntate.

Eugenio Caruso - 10 - 08 - 2021

Tratto da